Pontryagin space

A Hilbert space with an indefinite metric 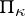that has a finite rank of indefiniteness 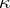. Basic facts concerning the geometry of these spaces were established by L.S. Pontryagin [1]. Besides the facts common for spaces with an indefinite metric, the following properties hold.

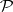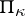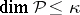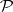If is an arbitrary non-negative linear manifold in , then ; if is a positive linear manifold and 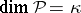, then its 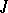-orthogonal complement 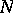is a negative linear manifold and 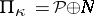. Moreover, 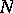is a complete space with respect to the norm 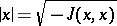. If the linear manifold 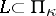is non-degenerate, then its 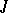-orthogonal complement 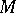is non-degenerate as well and .

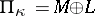The spectrum (in particular, the discrete spectrum) of a 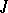-unitary (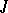-self-adjoint) operator is symmetric with respect to the unit circle (real line), all elementary divisors corresponding to eigen values 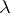, , 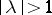are of finite order 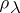, , 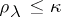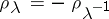. The sum of the dimensions of the root subspaces of a 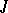-unitary (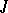-self-adjoint) operator corresponding to eigen values 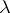, 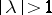(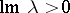), does not exceed .

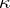The following theorem [1] is fundamental in the theory of 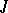-self-adjoint operators on a Pontryagin space 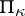: For each 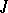-self-adjoint operator 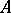(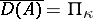) there exists a 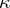-dimensional (maximal) non-negative invariant subspace 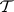in which all eigen values of 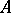have non-negative imaginary parts, and a 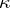-dimensional non-negative invariant subspace 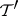in which all eigen values have non-positive imaginary parts. A similar statement in which the upper (lower) half-plane is replaced by the exterior (interior) of the unit disc is also valid for 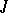-unitary operators, and under certain additional conditions — even for operators on the space .

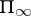If 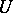is a 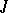-unitary operator, then its maximal invariant subspaces 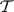, 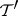can be chosen so that the elementary divisors of the operator 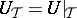, 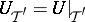are of minimal order. In order that a polynomial 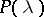with no roots inside the unit disc has the property: 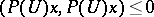, , 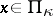it is necessary and sufficient that it can be divided by the minimal annihilating polynomial of the operator 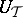. If 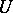is a cyclic operator, then its non-negative invariant subspaces of dimension 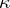are uniquely determined. In this case the above-mentioned property of the polynomial 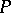with roots 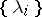outside the unit disc, 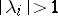, is equivalent to the divisibility of 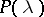by the characteristic polynomial of .

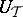Each completely-continuous 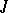-self-adjoint operator 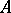on a Pontryagin space 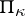such that zero belongs to its continuous spectrum does not have a residual spectrum. The root vectors of such an operator form a Riesz basis in 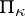with respect to the (definite) norm .

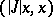Many facts concerning invariant subspaces and the spectrum can be generalized to a case of 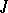-isometric and 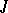-non-expanding operators. Thus, if 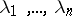is an arbitrary set of eigen values of a 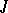-isometric operator, 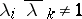, , 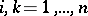and if 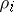is the order of the elementary divisor at the point 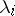, then 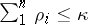. Any 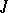-non-expanding boundedly-invertible operator 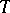has a 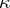-dimensional invariant non-negative subspace 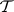such that all eigen values of the restriction 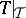lie in the unit disc [2]. A similar fact holds for maximal 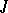-dissipative operators. In general, a 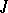-dissipative operator 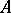, , 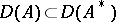has at most 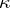eigen values in the upper half-plane. 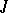-isometric and 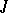-symmetric (and more generally, 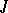-non-expanding and 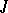-dissipative) operators are related by the Cayley transformation (cf. Cayley transform), which has on 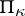all natural properties [2]. This fact allows one to develop the extension theory simultaneously for 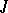-isometric and 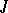-symmetric operators. In particular, every 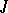-isometric (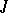-symmetric) operator can be extended to a maximal one. If its deficiency indices are different, then it has no 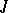-unitary (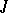-self-adjoint) extensions. If these indices are equal and finite, then any maximal extension is 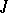-unitary (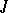-self-adjoint).

For completely-continuous operators on 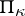, a number of statements on the completeness of the system of root vectors, analogous to the corresponding facts from the theory of dissipative operators on spaces with a definite metric, is valid.

References

[1]	L.S. Pontryagin, "Hermitian operators in a space with indefinite metric" Izv. Akad. Nauk. SSSR Ser. Mat. , 8 (1944) pp. 243–280 (In Russian)
[2]	I.S. Iokhvidov, M.G. Krein, "Spectral theory of operators in a space with indefinite metric I" Transl. Amer. Math. Soc. (2) , 13 (1960) pp. 105–175 Trudy Moskov. Mat. Obshch. , 5 (1956) pp. 367–432
[3]	I.S. Iokhvidov, M.G. Krein, "Spectral theory of operators in a space with indefinite metric II" Trudy Moskov. Mat. Obshch. , 8 (1959) pp. 413–496 (In Russian)
[4]	T.Ya. Azizov, I.S. Iokhvidov, "Linear operators in Hilbert spaces with 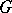-metric" Russian Math. Surveys , 26 : 4 (1971) pp. 45–97 Uspekhi Mat. Nauk , 26 : 4 (1971) pp. 43–92
[5]	M.G. Krein, "Introduction to the geometry of indefinite 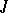-spaces and the theory of operators in these spaces" , Second Math. Summer School , 1 , Kiev (1965) pp. 15–92 (In Russian)
[6]	M.A. Naimark, R.S. Ismagilov, "Representations of groups and algebras in a space with indefinite metric" Itogi Nauk. i Tekhn. Mat. Anal. (1969) pp. 73–105 (In Russian)
[7]	L. Nagy, "State vector spaces with indefinite metric in quantum field theory" , Noordhoff (1966)

Comments

Pontryagin spaces form a subclass of the class of Krein spaces (cf. Krein space and also Hilbert space with an indefinite metric). The operator 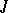appearing in the beginning of the main article above is the fundamental symmetry (see Krein space), which defines the indefinite inner product via the formula .

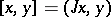References

[a1]	T.Ya. Azizov, I.S. [I.S. Iokhvidov] Iohidov, "Linear operators in spaces with an indefinite metric" , Wiley (1989) (Translated from Russian)
[a2]	I.S. [I.S. Iokhvidov] Iohidov, M.G. Krein, H. Langer, "Introduction to the spectral theory of operators in spaces with an indefinite metric" , Akademie Verlag (1982)