Point of inflection

A point 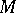on a planar curve having the following properties: at 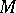the curve has a unique tangent, and within a small neighbourhood around 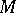the curve lies within one pair of vertical angles formed by the tangent and the normal (Fig. a). normal tangent

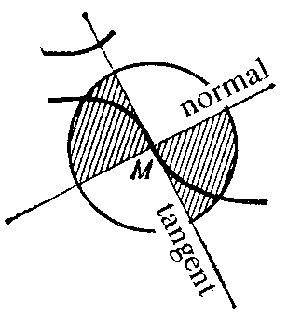
Figure: p073190a

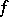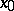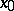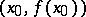Let a function be defined in a certain neighbourhood around a point and let it be continuous at that point. The point is called a point of inflection for if it is simultaneously the end of a range of strict convexity upwards and the end of a range of strict convexity downwards. In that case the point is called a point of inflection on the graph of the function, i.e. the graph of at 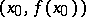"inflects" through the tangent to it at that point; for 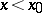the tangent lies under the graph of 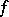, while for 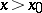it lies above that graph (or vice versa, Fig. b).

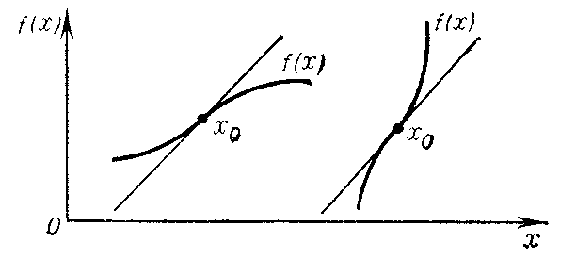
Figure: p073190b

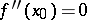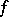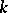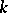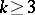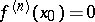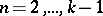A necessary existence condition for a point of inflection is: If is twice differentiable in some neighbourhood of a point , and if is a point of inflection, then . A sufficient existence condition for a point of inflection is: If is times continuously differentiable in a certain neighbourhood of a point , with odd and , while for , and 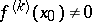, then 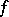has a point of inflection at .

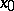References

[1]	V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 2 , MIR (1982) (Translated from Russian)
[2]	L.D. Kudryavtsev, "A course in mathematical analysis" , 1 , Moscow (1981) (In Russian)

References

[a1]	M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French)
[a2]	J.L. Coolidge, "Algebraic plane curves" , Dover, reprint (1959)