Pfaffian form

A differential form of degree 1.

Comments

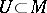A Pfaffian form defined on an open subset , a manifold, is of odd class 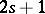at if it satisfies

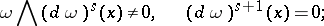it is of even class at if it satisfies

Pfaffian forms of class 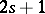and 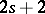both define a Pfaffian equation of class .

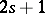Darboux's theorem on Pfaffian forms says the following.

1) If 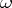is a Pfaffian form of constant class 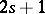on an open subset 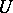of a manifold 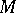, then for every 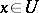there is a neighbourhood 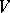with a family of independent functions 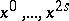, such that on ,

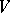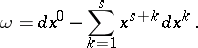2) If 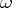is a Pfaffian form of constant class 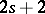on an open subset 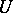of a manifold 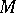, then for every 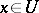there is a neighbourhood 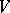with a family of independent functions 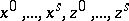such that on ,

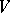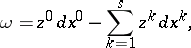where the function 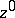is without zeros on .

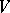Thus, if 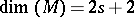, the functions 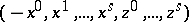are canonical coordinates for the symplectic form .

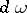References

[a1]	P. Libermann, C.-M. Marle, "Symplectic geometry and analytical mechanics" , Reidel (1987) pp. Chapt. V (Translated from French)