Perron transformation

An orthogonal (unitary) transformation

(1)

smoothly depending on and transforming a linear system of ordinary differential equations

(2)

to a system of triangular type

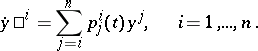(3)

It was introduced by O. Perron [1]. Perron's theorem applies: For any linear system (2) with continuous coefficients , a Perron transformation exists.

A Perron transformation is constructed by means of Gram–Schmidt orthogonalization (for each ) of the vector system , where 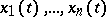is some fundamental system of solutions to (2), where different fundamental systems give, in general, different Perron transformations [1], [2]. For systems (2) with bounded continuous coefficients, all the Perron transformations are Lyapunov transformations (cf. Lyapunov transformation).

If the matrix-valued function , , 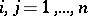is a recurrent function, one can find a recurrent matrix-valued function , , 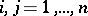such that (1) is the Perron transformation that reduces (2) to the triangular form (3), where, moreover, the function

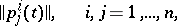is recurrent.

References

[1]	O. Perron, "Ueber eine Matrixtransformation" Math. Z. , 32 (1930) pp. 465–473
[2]	S.P. Diliberto, "On systems of ordinary differential equations" S. Lefschetz (ed.) et al. (ed.) , Contributions to the theory of nonlinear oscillations , Ann. Math. Studies , 20 , Princeton Univ. Press (1950) pp. 1–38
[3]	B.F. Bylov, R.E. Vinograd, D.M. Grobman, V.V. Nemytskii, "The theory of Lyapunov exponents and its applications to problems of stability" , Moscow (1966) (In Russian)
[4]	N.A. Izobov, "Linear systems of ordinary differential equations" J. Soviet Math. , 5 : 1 (1976) pp. 45–96 Itogi Nauk. i Tekhn. Mat. Anal. , 12 (1974) pp. 71–146