Perron-Frobenius theorem
Let a real square 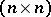 -matrix
-matrix 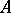 be considered as an operator on
be considered as an operator on 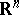 , let it be without invariant coordinate subspaces (such a matrix is called indecomposable) and let it be non-negative (i.e. all its elements are non-negative). Also, let
, let it be without invariant coordinate subspaces (such a matrix is called indecomposable) and let it be non-negative (i.e. all its elements are non-negative). Also, let  be its eigen values, enumerated such that
be its eigen values, enumerated such that
 |
Then,
1) the number  is a simple positive root of the characteristic polynomial of
is a simple positive root of the characteristic polynomial of  ;
;
2) there exists an eigen vector of 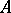 with positive coordinates corresponding to
with positive coordinates corresponding to  ;
;
3) the numbers  coincide, apart from their numbering, with the numbers
coincide, apart from their numbering, with the numbers  , where
, where  ;
;
4) the product of any eigen value of 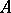 by
by 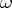 is an eigen value of
is an eigen value of  ;
;
5) for 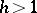 one can find a permutation of the rows and columns that reduces
one can find a permutation of the rows and columns that reduces  to the form
to the form
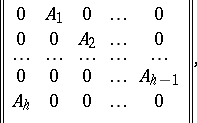 |
where 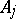 is a matrix of order
is a matrix of order  .
.
O. Perron proved the assertions 1) and 2) for positive matrices in [1], while G. Frobenius [2] gave the full form of the theorem.
References
| [1] | O. Perron, "Zur Theorie der Matrizen" Math. Ann. , 64 (1907) pp. 248–263 |
| [2] | G. Frobenius, "Ueber Matrizen aus nicht negativen Elementen" Sitzungsber. Königl. Preuss. Akad. Wiss. (1912) pp. 456–477 |
| [3] | F.R. [F.R. Gantmakher] Gantmacher, "The theory of matrices" , 1 , Chelsea, reprint (1977) (Translated from Russian) |
Comments
The Perron–Frobenius theorem has numerous applications, cf. [a1], [a2].
References
| [a1] | E. Seneta, "Nonnegative matrices" , Allen & Unwin (1973) |
| [a2] | K. Lancaster, "Mathematical economics" , Macmillan (1968) |
Perron-Frobenius theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Perron-Frobenius_theorem&oldid=48164