Permutation
of 
elements
A finite sequence of length 
in which all the elements are different, i.e. a permutation is an arrangement of 
elements without repetition. The number of permutations is 
.
Usually, one takes as the elements to be permuted the elements of the set 
; a one-to-one mapping 
of 
onto itself defines the permutation 
. The mapping 
is also called a substitution of 
. Many problems related to the enumeration of permutations are formulated in terms of substitutions, such as, for example, the enumeration of permutations with various restrictions on the positions of the permuted elements (cf. e.g. [1], [2]). A permutation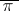 
can be regarded as an ordered set consisting of 
elements if one assumes that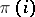 
precedes 
, 
.
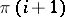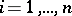Examples. 1) The pair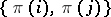 
forms an inversion in 
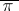if 
for 
; if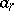 
is the number of permutations of 
elements with 
inversions, then
 |
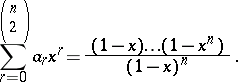2) If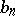 
is the number of permutations 
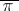consisting of 
elements such that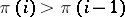 
for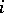 
even and 
for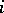 
odd, then
 |
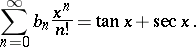Often a permutation is defined to be a bijective mapping of a finite set onto itself, i.e. a substitution (cf. also Permutation of a set).
References
| [1] | V.N. Sachkov, "Combinatorial methods in discrete mathematics" , Moscow (1977) (In Russian) |
| [2] | J. Riordan, "An introduction to combinational analysis" , Wiley (1958) |
Comments
See also Permutation group.
Permutation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Permutation&oldid=48160