Pascal distribution

A discrete probability distribution of a random variable 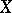taking non-negative integer values 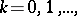in accordance with the formula

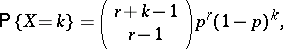where 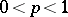and the integers 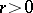are parameters.

The generating function and characteristic function of a Pascal distribution are

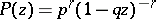and

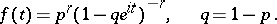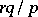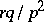The mathematical expectation and the variance are and , respectively.

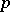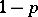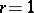The Pascal distribution with parameters and arises naturally in the scheme of the Bernoulli trial (cf. Bernoulli trials) with probability of "success" and of "failure" , as the distribution of the number of failures up to the occurrence of the -th success. For a Pascal distribution is the same as the geometric distribution with parameter 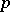, and for it is the same as the distribution of the sum of independent random variables having an identical geometric distribution with parameter . 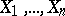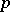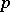Accordingly, the sum of independent random variables having Pascal distributions with parameters and , respectively, has the Pascal distribution with parameters and .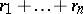

The distribution function of a Pascal distribution for 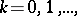is given by the formula

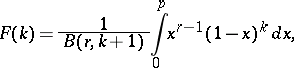where on the right-hand side there stands the value of the beta-distribution function at the point 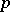(here 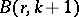is the beta-function). Using this relation one can define 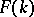for all 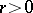. In this generalized sense a Pascal distribution is called a negative binomial distribution.

References

[1]	W. Feller, "An introduction to probability theory and its applications", 1 , Wiley (1957)

References

[a1]	N.L. Johnson, S. Kotz, "Distributions in statistics: discrete distributions" , Houghton Mifflin (1970)