Partial differential
of the first order of a function in several variables
The differential of the function with respect to one of the variables, keeping the remaining variables fixed. For example, if a function  is defined in some neighbourhood of a point
is defined in some neighbourhood of a point  , then the partial differential
, then the partial differential 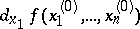 of
of  with respect to the variable
with respect to the variable  at the given point is equal to the ordinary differential
at the given point is equal to the ordinary differential  at
at  of the function
of the function 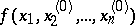 in the single variable
in the single variable  , i.e.
, i.e.
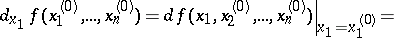 |
 |
It follows that
 |
Partial differentials of order  are defined analogously. For example, the partial differential
are defined analogously. For example, the partial differential  of order
of order 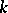 of
of  with respect to
with respect to  at
at 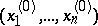 is just the
is just the  -th order differential of the function
-th order differential of the function  in the single variable
in the single variable  at the point
at the point  . Hence,
. Hence,
 |
 |
Comments
For references see Differential calculus and Differential.
Partial differential. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Partial_differential&oldid=48133