Parametric representation

of a function

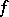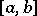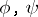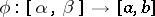The specification of a function , say defined on , by means of a pair of functions , say on , for which has a single-valued inverse 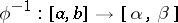such that 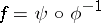, that is, for any ,

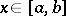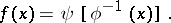Example. The pair of functions 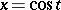, , 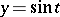, 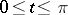is a parametric representation of the function , .

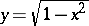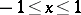If at a point 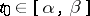a parametric representation of 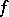is differentiable, that is, 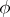and 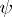are differentiable, and if 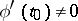, then 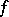is differentiable at 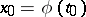and 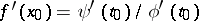. Furthermore, if 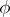and have at 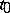derivatives of order , 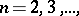then 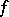has a derivative of order at 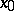, which is a fractional-rational function of the derivatives of 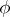and 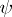of orders 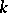, , 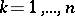where in the denominator there stands the 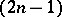-th power of 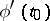; for example,

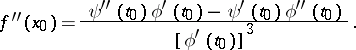Comments

The functions need not be real, the same as above holds for complex functions (i.e. , ).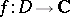

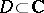References

[a1]	T.M. Apostol, "Calculus" , 1–2 , Blaisdell (1967)