A variant of the double-sweep method based on an orthogonal transformation of the unknowns. Let, for  , a boundary value problem be examined for a pair of linear ordinary differential equations
, a boundary value problem be examined for a pair of linear ordinary differential equations
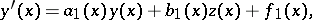 | (1) |
 | (2) |
with conditions of the form
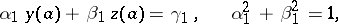 | (3) |
 | (4) |
Let the given functions 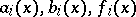 ,
,  , be continuous on the segment
, be continuous on the segment 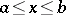 . A solution of the boundary value problem (1)–(4) by the orthogonal double-sweep method is realized as follows.
. A solution of the boundary value problem (1)–(4) by the orthogonal double-sweep method is realized as follows.
I) The auxiliary Cauchy problem
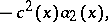 | (5) |
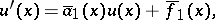 | (6) |
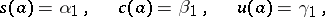 | (7) |
is solved, where
(the direct double-sweep).
II) The condition 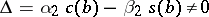 is tested, and if it is fulfilled, the Cauchy problem
is tested, and if it is fulfilled, the Cauchy problem
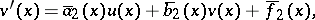 | (8) |
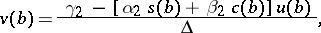 | (9) |
where
is solved in the direction from  to
to 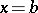 (the inverse double-sweep).
(the inverse double-sweep).
III) The required functions are calculated using the formulas
If the solution  of the boundary value problem (1)–(4) exists and is unique and stable with respect to small changes of the coefficients and the free terms defining the problem, then
of the boundary value problem (1)–(4) exists and is unique and stable with respect to small changes of the coefficients and the free terms defining the problem, then  and the method in question is also stable (see [2]).
and the method in question is also stable (see [2]).
A system of linear algebraic equations
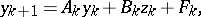 | (10) |
 | (11) |
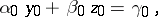 | (12) |
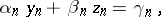 | (13) |
where 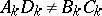 ,
, 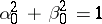 ,
,  , is solved according to the following rules.
, is solved according to the following rules.
1) Using the formulas
the quantities 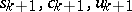 are calculated successively when
are calculated successively when  (the direct double-sweep).
(the direct double-sweep).
2) The condition 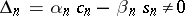 is tested, and if it is fulfilled, then
is tested, and if it is fulfilled, then
and
are calculated, when 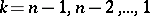 (inverse double-sweep).
(inverse double-sweep).
3) The values of the required solution of the system of equations (10)–(13) are calculated using the formulas
If a solution of the system of equations (10)–(13) exists and is unique and stable with respect to small changes of the coefficients and the free terms, then the orthogonal double-sweep method in question is also stable (see [2]).
Methods based on the use of a fundamental system of solutions of a homogeneous system of equations which aim at transferring the boundary conditions are sometimes called orthogonal double-sweep methods (see [1], [3]). However, these methods are really variants of the shooting method.
References
| [1] | N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian) |
| [2] | V.I. Krylov, V.V. Bobkov, P.I. Monastyrnyi, "Computing methods of higher mathematics" , 2 , Minsk (1975) (In Russian) |
| [3] | A.A. Samarskii, E.S. Nikolaev, "Numerical methods for grid equations" , 1–2 , Birkhäuser (1989) (Translated from Russian) |
Care should be taken with some steps in the above algorithm, as severe cancellation may occur (e.g. in 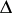 ). Also, the method requires solving non-linear equations, whereas the system is simple and linear. This aspect is also shared by the Riccati method (or invariant imbedding), which however uses one non-linear equation only. Other variants, with similar ideas as this "orthogonal double-sweep method" , are in [a2].
). Also, the method requires solving non-linear equations, whereas the system is simple and linear. This aspect is also shared by the Riccati method (or invariant imbedding), which however uses one non-linear equation only. Other variants, with similar ideas as this "orthogonal double-sweep method" , are in [a2].
References
| [a1] | U.M. Ascher, R.M.M. Mattheij, R.D. Russell, "Numerical solution for boundary value problems for ordinary differential equations" , Prentice-Hall (1988) |
| [a2] | G.M. Meyer, "Continuous orthonormalization for boundary value problems" J. Comput. Phys. , 62 (1986) pp. 248–262 |
How to Cite This Entry:
Orthogonal double-sweep method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Orthogonal_double-sweep_method&oldid=48074
This article was adapted from an original article by A.F. Shapkin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article , a boundary value problem be examined for a pair of linear ordinary differential equations
, a boundary value problem be examined for a pair of linear ordinary differential equations
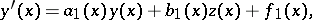

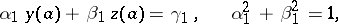

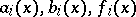 ,
,  , be continuous on the segment
, be continuous on the segment 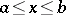 . A solution of the boundary value problem (1)–(4) by the orthogonal double-sweep method is realized as follows.
. A solution of the boundary value problem (1)–(4) by the orthogonal double-sweep method is realized as follows.
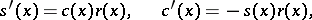

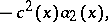
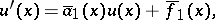
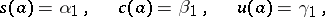

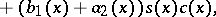
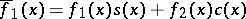
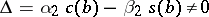 is tested, and if it is fulfilled, the Cauchy problem
is tested, and if it is fulfilled, the Cauchy problem
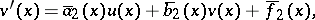
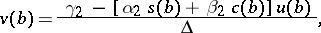

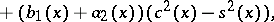
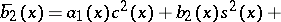
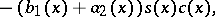
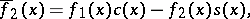
 to
to 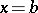 (the inverse double-sweep).
(the inverse double-sweep).

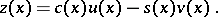
 of the boundary value problem (1)–(4) exists and is unique and stable with respect to small changes of the coefficients and the free terms defining the problem, then
of the boundary value problem (1)–(4) exists and is unique and stable with respect to small changes of the coefficients and the free terms defining the problem, then  and the method in question is also stable (see [2]).
and the method in question is also stable (see [2]).
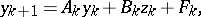

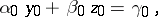
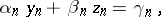
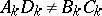 ,
, 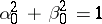 ,
,  , is solved according to the following rules.
, is solved according to the following rules.
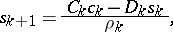
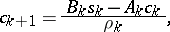
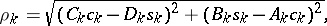
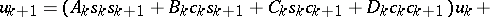
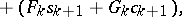

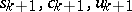 are calculated successively when
are calculated successively when  (the direct double-sweep).
(the direct double-sweep).
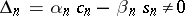 is tested, and if it is fulfilled, then
is tested, and if it is fulfilled, then
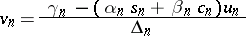

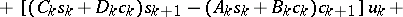
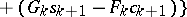
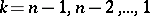 (inverse double-sweep).
(inverse double-sweep).

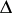 ). Also, the method requires solving non-linear equations, whereas the system is simple and linear. This aspect is also shared by the Riccati method (or invariant imbedding), which however uses one non-linear equation only. Other variants, with similar ideas as this "orthogonal double-sweep method" , are in [a2].
). Also, the method requires solving non-linear equations, whereas the system is simple and linear. This aspect is also shared by the Riccati method (or invariant imbedding), which however uses one non-linear equation only. Other variants, with similar ideas as this "orthogonal double-sweep method" , are in [a2].