Orderable group
A group  on which a total order
on which a total order  (cf. Totally ordered group) can be introduced such that
(cf. Totally ordered group) can be introduced such that  entails
entails  for any
for any  . A group
. A group  is orderable as a group if and only if there exists a subset
is orderable as a group if and only if there exists a subset  with the properties: 1)
with the properties: 1)  ; 2)
; 2)  , 3)
, 3)  ; 4)
; 4) 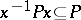 for any
for any  .
.
Let 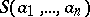 be the normal sub-semi-group of
be the normal sub-semi-group of 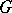 generated by
generated by  . The group
. The group 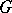 is orderable as a group if and only if for any finite set of elements
is orderable as a group if and only if for any finite set of elements  in
in 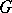 , different from the unit element, numbers
, different from the unit element, numbers  can be found, equal to
can be found, equal to 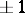 , such that the sub-semi-group
, such that the sub-semi-group 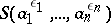 does not contain the unit element. Every orderable group is a group with unique root extraction. Abelian torsion-free groups, locally nilpotent torsion-free groups, free, and free solvable groups are orderable groups. Two-step solvable groups such that for every non-unit element
does not contain the unit element. Every orderable group is a group with unique root extraction. Abelian torsion-free groups, locally nilpotent torsion-free groups, free, and free solvable groups are orderable groups. Two-step solvable groups such that for every non-unit element  ,
, 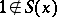 , are orderable groups.
, are orderable groups.
The class of orderable groups is closed under taking subgroups and direct products; it is locally closed, and consequently, a quasi-variety. A free product of orderable groups is again an orderable group.
References
| [1] | A.I. Kokorin, V.M. Kopytov, "Fully ordered groups" , Israel Program Sci. Transl. (1974) (Translated from Russian) |
| [2] | L. Fuchs, "Partially ordered algebraic systems" , Pergamon (1963) |
Orderable group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Orderable_group&oldid=48067