Optional sigma-algebra
From Encyclopedia of Mathematics
optional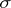 
-algebra
The smallest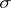 
-algebra 
of sets (cf. Algebra of sets) in 
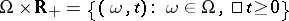generated by all mappings 
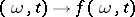of the set 
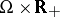into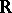 
which (for every fixed 
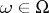) are continuous from the right (in 
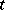), have limits from the left and are adapted to a (given) non-decreasing family 
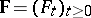of sub-
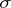-algebras 
, 
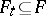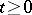, where 
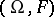is a measurable space. The optional 
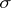-algebra coincides with the smallest 
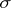-algebra generated by the stochastic intervals 
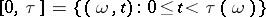, where 
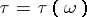are stopping times (relative to 
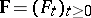) (cf. Markov moment). The inclusion 
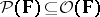holds between the optional and predictable 
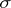-algebras (cf. Predictable sigma-algebra).
References
| [1] | C. Dellacherie, "Capacités et processus stochastiques" , Springer (1972) |
Comments
In [a1] the optional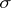 
-field is called the well-measurable 
-field.
References
| [a1] | C. Dellacherie, P.A. Meyer, "Probabilities and potential" , A , North-Holland (1978) (Translated from French) |
How to Cite This Entry:
Optional sigma-algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Optional_sigma-algebra&oldid=48061
Optional sigma-algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Optional_sigma-algebra&oldid=48061
This article was adapted from an original article by A.N. Shiryaev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article