Operator group
A group of operators, a one-parameter group of operators (cf. Operator) on a Banach space 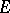 , i.e. a family of bounded linear operators
, i.e. a family of bounded linear operators 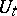 ,
, 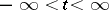 , such that
, such that 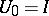 ,
, 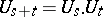 and
and 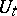 depends continuously on
depends continuously on 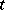 (in the uniform, strong or weak topology). If
(in the uniform, strong or weak topology). If 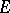 is a Hilbert space and
is a Hilbert space and 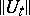 is uniformly bounded, then the group
is uniformly bounded, then the group 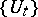 is similar to a group of unitary operators (Sz.-Nagy's theorem, cf. also Unitary operator).
is similar to a group of unitary operators (Sz.-Nagy's theorem, cf. also Unitary operator).
References
| [1] | B. Szökevalfi-Nagy, "On uniformly bounded linear transformations in Hilbert space" Acta Sci. Math. (Szeged) , 11 (1947) pp. 152–157 |
| [2] | E. Hille, R.S. Phillips, "Functional analysis and semi-groups" , Amer. Math. Soc. (1948) |
V.I. Lomonosov
A group with operators, a group with domain of operators 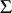 , where
, where 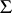 is a set of symbols, is a group
is a set of symbols, is a group 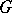 such that for every element
such that for every element 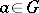 and every
and every 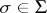 there is a corresponding element
there is a corresponding element 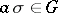 such that
such that 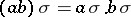 for any
for any 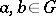 . Let
. Let 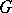 and
and 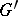 be groups with the same domain of operators
be groups with the same domain of operators 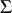 ; an isomorphic (a homomorphic) mapping
; an isomorphic (a homomorphic) mapping 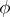 of
of 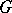 onto
onto 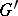 is called an operator isomorphism (operator homomorphism) if
is called an operator isomorphism (operator homomorphism) if 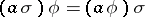 for any
for any 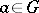 ,
, 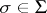 . A subgroup (normal subgroup)
. A subgroup (normal subgroup) 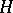 of the group
of the group 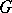 with domain of operators
with domain of operators 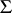 is called an admissible subgroup (admissible normal subgroup) if
is called an admissible subgroup (admissible normal subgroup) if 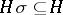 for any
for any 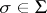 . The intersection of all admissible subgroups containing a given subset
. The intersection of all admissible subgroups containing a given subset 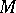 of
of 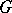 is called the admissible subgroup generated by the set
is called the admissible subgroup generated by the set 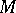 . A group which does not have admissible normal subgroups apart from itself and the trivial subgroup is called a simple group (with respect to the given domain of operators). Every quotient group of an operator group by an admissible normal subgroup is a group with the same domain of operators.
. A group which does not have admissible normal subgroups apart from itself and the trivial subgroup is called a simple group (with respect to the given domain of operators). Every quotient group of an operator group by an admissible normal subgroup is a group with the same domain of operators.
A group 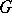 is called a group with a semi-group of operators
is called a group with a semi-group of operators 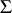 if
if 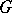 is a group with domain of operators
is a group with domain of operators 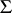 ,
, 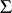 is a semi-group and
is a semi-group and 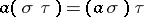 for any
for any 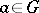 ,
, 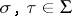 . If
. If 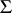 is a semi-group with an identity element
is a semi-group with an identity element  , it is supposed that
, it is supposed that 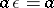 for every
for every 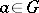 . Every group with an arbitrary domain of operators
. Every group with an arbitrary domain of operators 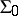 is a group with semi-group of operators
is a group with semi-group of operators 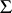 , where
, where 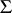 is the free semi-group generated by the set
is the free semi-group generated by the set 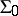 . A group
. A group 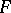 with semi-group of operators
with semi-group of operators 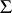 possessing an identity element is called
possessing an identity element is called 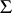 -free if it is generated by a system of elements
-free if it is generated by a system of elements 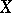 such that the elements
such that the elements 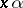 , where
, where 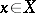 ,
, 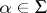 , constitute for
, constitute for 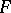 (as a group without operators) a system of free generators. Let
(as a group without operators) a system of free generators. Let 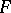 be a
be a 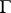 -free group (
-free group (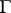 being a group of operators), let
being a group of operators), let  be a subgroup of
be a subgroup of 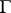 , let
, let 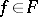 , and let
, and let 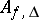 be the admissible subgroup of
be the admissible subgroup of 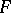 generated by all elements of the form
generated by all elements of the form 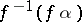 , where
, where 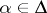 . Then every admissible subgroup of
. Then every admissible subgroup of 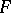 is an operator free product of groups of type
is an operator free product of groups of type 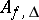 and a
and a 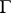 -free group (see [2]). If
-free group (see [2]). If 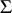 is a free semi-group of operators, then, if
is a free semi-group of operators, then, if 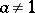 , the admissible subgroup of the
, the admissible subgroup of the 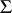 -free group
-free group 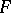 generated by the element
generated by the element  is itself a
is itself a 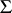 -free group with free generator
-free group with free generator  (see also ).
(see also ).
An Abelian group with an associative ring of operators  is just a
is just a 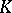 -module (cf. Module).
-module (cf. Module).
References
| [1] | A.G. Kurosh, "The theory of groups" , 1–2 , Chelsea (1955–1956) (Translated from Russian) |
| [2] | S.T. Zavalo, "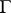 -free operator groups" Mat. Sb. , 33 (1953) pp. 399–432 (In Russian) -free operator groups" Mat. Sb. , 33 (1953) pp. 399–432 (In Russian) |
| [3a] | S.T. Zavalo, "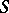 -free operator groups I" Ukr. Mat. Zh. , 16 : 5 (1964) pp. 593–602 (In Russian) -free operator groups I" Ukr. Mat. Zh. , 16 : 5 (1964) pp. 593–602 (In Russian) |
| [3b] | S.T. Zavalo, "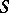 -free operator groups II" Ukr. Mat. Zh. , 16 : 6 (1964) pp. 730–751 (In Russian) -free operator groups II" Ukr. Mat. Zh. , 16 : 6 (1964) pp. 730–751 (In Russian) |
Operator group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Operator_group&oldid=48049