One-parameter transformation group

flow

The action of the additive group of real numbers on a manifold .

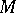Thus, a one-parameter family 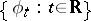of transformations of a manifold 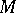is a one-parameter transformation group if the following conditions are satisfied:

(*)

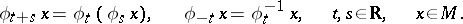If the manifold 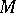is smooth, then the group is usually assumed to be smooth also, that is, the corresponding mapping

is a differentiable mapping of differentiable manifolds.

A more general concept is that of a local one-parameter transformation group of a manifold 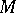. It is defined as a mapping 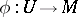of some open submanifold of the form 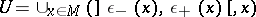, where 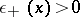, for 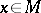, satisfying the conditions (*) for all 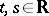, 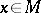for which both sides of the equations are defined.

With each smooth local one-parameter transformation group 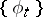of 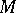one associates the vector field

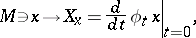called the velocity field, or infinitesimal generator, of the group 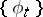. Conversely, any smooth vector field 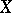generates a local one-parameter transformation group 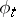having velocity field 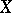. In local coordinates 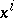on 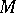this one-parameter transformation group is given as the solution of the system of ordinary differential equations

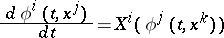with the initial conditions 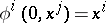, where .

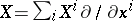If the local one-parameter transformation group generated by the vector field 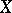can be extended to a global one, then the field 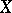is called complete. On a compact manifold any vector field is complete, so that there is a one-to-one correspondence between one-parameter transformation groups and vector fields. This is not the case for non-compact manifolds, and the set of complete vector fields is not even closed under addition.

References

[1]	V.I. Arnol'd, "Ordinary differential equations" , M.I.T. (1973) (Translated from Russian)
[2]	R. Palais, "A global formulation of the Lie theory of transformation groups" , Amer. Math. Soc. (1957)

References

[a1]	G.R. Sell, "Topological dynamics and ordinary differential equations" , v. Nostrand-Reinhold (1971)