Object in a category

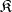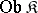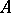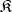A term used to denote elements of an arbitrary category, playing the role of sets, groups, topological spaces, etc. An object in a category is an undefined concept. Every category consists of elements of two classes, the class of objects and the class of morphisms. The class of objects of a category is usually denoted by . With any object of there is associated a unique identity morphism 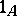, so that different identity morphisms correspond to different objects. Hence the concept of a category can be formally defined by means of morphisms alone. However, the term "object in a category" is a linguistic convenience which is practically always used. The division of the elements of a category into objects and morphisms is only meaningful within a fixed category, since the objects of one category can be the morphisms of another. Thanks to the presence of morphisms, interrelations can be defined between the objects of a category, allowing one to single out special classes of objects (cf. Integral object of a category; Null object of a category; Small object; Projective object of a category; Injective object; etc.).

Comments

Cf. also Generator of a category.