Nuisance parameter
Any unknown parameter of a probability distribution in a statistical problem connected with the study of other parameters of a given distribution. More precisely, for a realization of a random variable 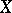 , taking values in a sample space
, taking values in a sample space 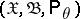 ,
, 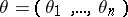 ,
, 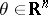 , suppose it is necessary to make a statistical inference about the parameters
, suppose it is necessary to make a statistical inference about the parameters 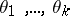 ,
, 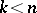 . Then
. Then 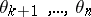 are nuisance parameters in the problem. For example, let
are nuisance parameters in the problem. For example, let 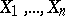 be independent random variables, subject to the normal law
be independent random variables, subject to the normal law 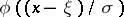 , with unknown parameters
, with unknown parameters 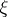 and
and 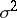 , and one wishes to test the hypothesis
, and one wishes to test the hypothesis 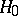 :
: 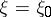 , where
, where 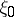 is some fixed number. The unknown variance
is some fixed number. The unknown variance 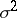 is a nuisance parameter in the problem of testing
is a nuisance parameter in the problem of testing 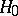 . Another important example of a problem with a nuisance parameter is the Behrens–Fisher problem. Naturally, for the solution of a statistical problem with nuisance parameters it is desirable to be able to make a statistical inference not depending on these parameters. In the theory of statistical hypothesis testing one often achieves this by narrowing the class of tests intended for testing a certain hypothesis
. Another important example of a problem with a nuisance parameter is the Behrens–Fisher problem. Naturally, for the solution of a statistical problem with nuisance parameters it is desirable to be able to make a statistical inference not depending on these parameters. In the theory of statistical hypothesis testing one often achieves this by narrowing the class of tests intended for testing a certain hypothesis 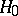 in the presence of a nuisance parameter to a class of similar tests (cf. Statistical test).
in the presence of a nuisance parameter to a class of similar tests (cf. Statistical test).
References
| [1] | Yu.V. Linnik, "Statistical problems with nuisance parameters" , Amer. Math. Soc. (1968) (Translated from Russian) |
Comments
References
| [a1] | E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1978) |
| [a2] | E.L. Lehmann, "Theory of point estimation" , Wiley (1983) |
Nuisance parameter. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nuisance_parameter&oldid=48028