Normal fundamental system of solutions

of a linear homogeneous system of ordinary differential equations

A fundamental system of solutions 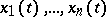such that any other fundamental system 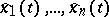satisfies the inequality

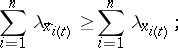here

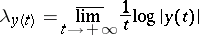is the Lyapunov characteristic exponent of a solution . Normal fundamental systems of solutions were introduced by A.M. Lyapunov [1], who proved that they exist for every linear system

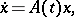where 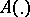is a mapping

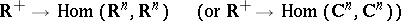that is summable on every segment and satisfies the additional condition

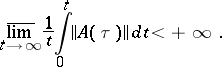References

[1]	A.M. Lyapunov, "Collected works" , 1–5 , Moscow-Leningrad (1956) (In Russian)