Normal convergence
Convergence of a series
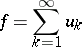 | (1) |
formed by bounded mappings  from a set
from a set  into a normed space
into a normed space  , such that the series with positive terms
, such that the series with positive terms  formed by the norms of the mappings,
formed by the norms of the mappings,
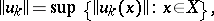 |
converges.
Normal convergence of the series (1) implies absolute and uniform convergence of the series  consisting of elements of
consisting of elements of  ; the converse is not true. For example, if
; the converse is not true. For example, if  is the real-valued function defined by
is the real-valued function defined by 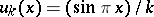 for
for 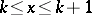 and
and 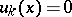 for
for  , then the series
, then the series  converges absolutely, whereas
converges absolutely, whereas 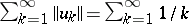 diverges.
diverges.
Suppose, in particular, that each 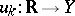 is a piecewise-continuous function on a non-compact interval
is a piecewise-continuous function on a non-compact interval 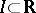 and that (1) converges normally. Then one can integrate term-by-term on
and that (1) converges normally. Then one can integrate term-by-term on  :
:
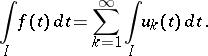 |
Let 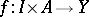 , where
, where 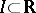 is an interval, have left and right limits at each point of
is an interval, have left and right limits at each point of  . Then the improper integral
. Then the improper integral
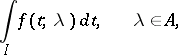 | (2) |
is called normally convergent on  if there exists a piecewise-continuous positive function
if there exists a piecewise-continuous positive function 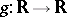 such that: 1)
such that: 1) 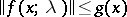 for any
for any  and any
and any 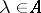 ; and 2) the integral
; and 2) the integral 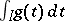 converges. Normal convergence of (2) implies its absolute and uniform convergence; the converse is not true.
converges. Normal convergence of (2) implies its absolute and uniform convergence; the converse is not true.
References
| [1] | N. Bourbaki, "Elements of mathematics. General topology" , Addison-Wesley (1966) (Translated from French) |
| [2] | N. Bourbaki, "Elements of mathematics. Functions of a real variable" , Addison-Wesley (1976) (Translated from French) |
| [3] | L. Schwartz, "Cours d'analyse" , 1 , Hermann (1967) |
Normal convergence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Normal_convergence&oldid=48009