Non-linear differential equation
A differential equation (ordinary or partial) in which at least one of the derivatives of the unknown function (including the derivative of order zero: the function itself) occurs non-linearly. This term is used, as a rule, when one wishes to emphasize especially that the equation 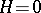 in question is not linear, that is, its left-hand side
in question is not linear, that is, its left-hand side 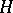 is not a linear form in the derivatives of the unknown function with coefficients depending only on the independent variables.
is not a linear form in the derivatives of the unknown function with coefficients depending only on the independent variables.
Sometimes by a non-linear differential equation one means a more general equation of a certain form. For example, a non-linear ordinary first-order differential equation is an equation
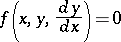 |
with an arbitrary function 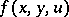 ; here a linear ordinary first-order differential equation corresponds to the special case
; here a linear ordinary first-order differential equation corresponds to the special case
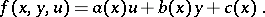 |
A non-linear partial first-order differential equation for an unknown function  in
in  independent variables
independent variables  has the form
has the form
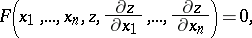 |
where  is an arbitrary function of its arguments; when
is an arbitrary function of its arguments; when
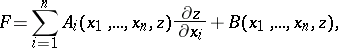 |
such an equation is called quasi-linear, and when
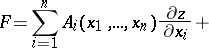 |
 |
it is called linear (cf. also Linear partial differential equation; Non-linear partial differential equation).
Non-linear differential equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Non-linear_differential_equation&oldid=47992