Nevanlinna theorems
Two fundamental theorems, proved by R. Nevanlinna (see [1], [2]), that are basic for the theory of value distribution of meromorphic functions (see Value-distribution theory). Let 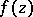 be a meromorphic function on a disc
be a meromorphic function on a disc
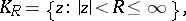 |
where  means that
means that 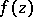 is meromorphic in the entire open complex plane. For every
is meromorphic in the entire open complex plane. For every  ,
, 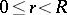 , the proximity function of
, the proximity function of 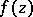 to a number
to a number  is defined by
is defined by
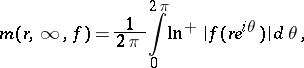 |
 |
and the counting function of the number of  -points of
-points of 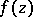 by
by
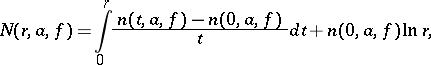 |
where  denotes the number of
denotes the number of  -points of
-points of  , counting multiplicities, in the disc
, counting multiplicities, in the disc 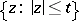 , i.e. the number of elements of
, i.e. the number of elements of  , and
, and 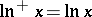 for
for 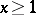 ,
,  for
for 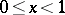 .
.
The function 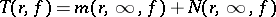 is called the Nevanlinna characteristic of
is called the Nevanlinna characteristic of 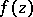 .
.
Nevanlinna's first theorem. For any function  that is meromorphic on a disc
that is meromorphic on a disc 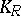 , for any
, for any  ,
, 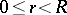 , and any complex number
, and any complex number  ,
,
 | (1) |
where
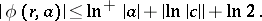 |
Here  denotes the first non-zero coefficient in the Laurent expansion about zero of the function
denotes the first non-zero coefficient in the Laurent expansion about zero of the function 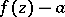 if
if 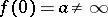 , and of
, and of 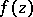 itself if
itself if 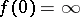 . Thus, for a function whose characteristic
. Thus, for a function whose characteristic 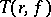 increases without limit as
increases without limit as 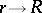 , the sum
, the sum 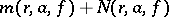 , considered for different values of
, considered for different values of  , is equal to the value
, is equal to the value 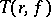 up to a bounded additive term
up to a bounded additive term 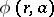 . In this sense, all values
. In this sense, all values  are equivalent for any function
are equivalent for any function 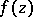 that is meromorphic on
that is meromorphic on  . For this reason, the theory of value distribution of meromorphic functions concerns itself with questions about the asymptotic behaviour of one term,
. For this reason, the theory of value distribution of meromorphic functions concerns itself with questions about the asymptotic behaviour of one term, 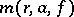 or
or 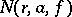 , in the invariant sum (1).
, in the invariant sum (1).
Nevanlinna's second theorem shows that, for almost all points  , the principal role in the sum (1) is played by
, the principal role in the sum (1) is played by  . The statement of the theorem is as follows.
. The statement of the theorem is as follows.
For any function 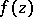 that is meromorphic on a disc
that is meromorphic on a disc 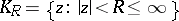 , every
, every 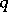 ,
, 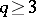 , and any distinct numbers
, and any distinct numbers  in the extended complex plane, the relation
in the extended complex plane, the relation
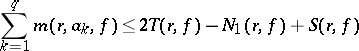 | (2) |
holds, where
 |
and the term 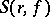 has the following properties:
has the following properties:
1) If  , i.e. if
, i.e. if 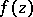 is meromorphic in the entire open complex plane, then
is meromorphic in the entire open complex plane, then
 |
as  , for all values of
, for all values of  with the possible exception of a set
with the possible exception of a set 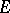 of finite total measure.
of finite total measure.
2) If 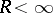 , then
, then
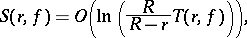 |
as  , for all values of
, for all values of  with the possible exception of a set
with the possible exception of a set 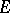 for which
for which
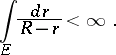 |
The function 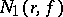 is non-decreasing with increasing
is non-decreasing with increasing  , and therefore the right-hand term in (2) cannot increase as
, and therefore the right-hand term in (2) cannot increase as 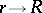 more rapidly than
more rapidly than  outside some exceptional set
outside some exceptional set 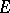 .
.
References
| [1] | R. Nevanilinna, "Analytic functions" , Springer (1970) (Translated from German) |
| [2] | R. Nevanlinna, "Le théorème de Picard–Borel et la théorie des fonctions méromorphes" , Gauthier-Villars (1929) |
| [3] | H. Weyl, "Meromorphic functions and analytic curves" , Princeton Univ. Press (1943) |
| [4] | L. Ahlfors, "The theory of meromorphic curves" Acta Soc. Sci. Fennica. Nova Ser. A , 3 : 4 (1941) pp. 1–31 |
| [5] | H. Cartan, "Sur les zéros des combinations linéares de 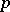 fonctions holomorphes données" Mathematica (Cluj) , 7 (1933) pp. 5–31 fonctions holomorphes données" Mathematica (Cluj) , 7 (1933) pp. 5–31 |
| [6] | P. Griffiths, J. King, "Nevanlinna theory and holomorphic mappings between algebraic varieties" Acta Math. , 130 (1973) pp. 145–220 |
| [7] | V.P. Petrenko, "The growth of meromorphic functions" , Khar'kov (1978) (In Russian) |
Comments
References
| [a1] | W.K. Hayman, "Meromorphic functions" , Oxford Univ. Press (1964) |
| [a2] | P.A. Griffiths, "Entire holomorphic mappings in one and several complex variables" , Annals Math. Studies , 85 , Princeton Univ. Press (1976) |
Nevanlinna theorems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nevanlinna_theorems&oldid=47963