Net (directed set)
From Encyclopedia of Mathematics
A mapping of a directed set into a (topological) space.
Comments
The topology of a space can be described completely in terms of convergence. However, this needs a more general concept of convergence than the concept of convergence of a sequence. What is needed is convergence of nets. A net 
in a topological space 
converges to a point 
if for each open neighbourhood 
of 
in 
the net 
is eventually in 
. The last phrase means that there is an 
such that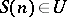 
for all 
in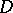 
.
The theory of convergence of nets is known as Moore–Smith convergence, [a1].
References
| [a1] | J.L. Kelley, "General topology" , v. Nostrand (1955) pp. Chapt. II |
How to Cite This Entry:
Net (directed set). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Net_(directed_set)&oldid=47955
Net (directed set). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Net_(directed_set)&oldid=47955
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article