Negative polynomial distribution
negative multinomial distribution
The joint probability distribution (cf. also Joint distribution) of random variables 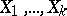 that take non-negative integer values
that take non-negative integer values 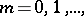 defined by the formula
defined by the formula
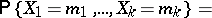 | (*) |
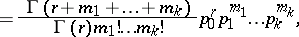 |
where 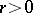 and
and 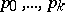 (
(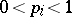 ,
, 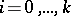 ;
; 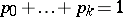 ) are parameters. A negative multinomial distribution is a multi-dimensional discrete distribution — a distribution of a random vector
) are parameters. A negative multinomial distribution is a multi-dimensional discrete distribution — a distribution of a random vector 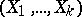 with non-negative integer components.
with non-negative integer components.
The generating function of the negative polynomial distribution with parameters 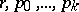 has the form
has the form
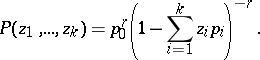 |
A negative multinomial distribution arises in the following multinomial scheme. Successive independent trials are carried out, and in each trial 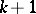 different outcomes with labels
different outcomes with labels 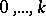 are possible, having probabilities
are possible, having probabilities 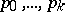 , respectively. The trials continue up to the
, respectively. The trials continue up to the  -th appearance of the outcome with label 0 (here
-th appearance of the outcome with label 0 (here  is an integer). If
is an integer). If 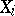 is the number of appearances of the outcome with label
is the number of appearances of the outcome with label 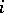 ,
, 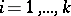 , during the trials, then formula (*) expresses the probability of the appearance of outcomes with labels
, during the trials, then formula (*) expresses the probability of the appearance of outcomes with labels 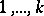 , equal, respectively,
, equal, respectively,  times, up to the
times, up to the  -th appearance of the outcome 0. A negative multinomial distribution in this sense is a generalization of a negative binomial distribution, coinciding with it when
-th appearance of the outcome 0. A negative multinomial distribution in this sense is a generalization of a negative binomial distribution, coinciding with it when 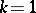 .
.
If a random vector 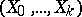 has, conditionally on
has, conditionally on  , a multinomial distribution with parameters
, a multinomial distribution with parameters 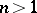 ,
, 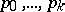 and if the parameter
and if the parameter  is itself a random variable having a negative binomial distribution with parameters
is itself a random variable having a negative binomial distribution with parameters 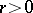 ,
, 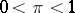 , then the marginal distribution of the vector
, then the marginal distribution of the vector 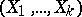 , given the condition
, given the condition 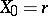 , is the negative multinomial distribution with parameters
, is the negative multinomial distribution with parameters  ,
, 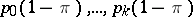 .
.
Comments
References
| [a1] | J. Neyman, "Proceedings of the international symposium on discrete distributions" , Montreal (1963) |
Negative polynomial distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Negative_polynomial_distribution&oldid=47953