Natural coordinate frame
From Encyclopedia of Mathematics
Frénet trihedron, Frénet frame, natural trihedron
A figure consisting of the tangent, the principal normal and the binormal of a space curve, and the three planes defined by the pairs of these straight lines. If the edges of the natural frame at a given point of a curve are taken as the axes of a Cartesian coordinate system, the equation of the curve in the natural parametrization (see Natural parameter) is, in a neighbourhood of that point,
 |
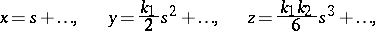where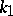 
and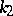 
are the curvature and torsion of the curve at the point.
Comments
Cf. also Frénet trihedron.
References
| [a1] | W. Klingenberg, "A course in differential geometry" , Springer (1978) (Translated from German) |
| [a2] | W. Blaschke, K. Leichtweiss, "Elementare Differentialgeometrie" , Springer (1977) |
How to Cite This Entry:
Natural coordinate frame. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Natural_coordinate_frame&oldid=47948
Natural coordinate frame. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Natural_coordinate_frame&oldid=47948
This article was adapted from an original article by A.B. Ivanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article