Müntz theorem
theorem on the completeness of a system of powers 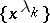 on an interval
on an interval 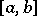 ,
, 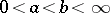
Let 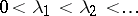 . In order that for any continuous function
. In order that for any continuous function 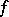 on
on 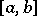 and for any
and for any 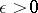 there is a linear combination
there is a linear combination
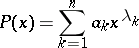 |
such that
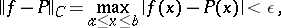 |
it is necessary and sufficient that
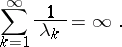 | (*) |
In the case of an interval 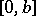 one adds the function which is identically equal to 1 to the system
one adds the function which is identically equal to 1 to the system 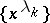 and condition (*) is, as before, necessary and sufficient for the completeness of the enlarged system. The condition
and condition (*) is, as before, necessary and sufficient for the completeness of the enlarged system. The condition 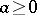 is essential: the system
is essential: the system  (which satisfies (*)) is not complete on
(which satisfies (*)) is not complete on 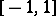 (an odd function cannot be arbitrarily closely approximated by combinations of even powers).
(an odd function cannot be arbitrarily closely approximated by combinations of even powers).
Condition (*) is necessary and sufficient for the completeness of 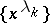 ,
, 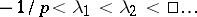 , on
, on 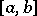 ,
,  , in the metric of
, in the metric of 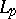 ,
, 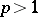 ; that is, for each
; that is, for each 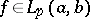 and any
and any 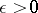 there is a linear combination
there is a linear combination 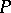 such that
such that
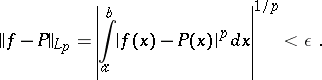 |
The theorem was proved by H. Müntz [1].
References
| [1] | H. Müntz, "Ueber den Approximationssatz von Weierstrass" , Festschrift H.A. Schwarz , Schwarz–Festschrift , Berlin (1914) |
| [2] | N.I. [N.I. Akhiezer] Achiezer, "Theory of approximation" , F. Ungar (1956) (Translated from Russian) |
Comments
There exists several extensions of the Müntz theorem. First, O. Szász showed that with exponents  ,
, 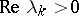 ,
,
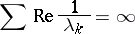 | (a1) |
is necessary and sufficient for completeness of the system 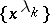 in
in 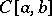 or
or 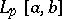 ,
, 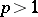 , or, equivalently, completeness of
, or, equivalently, completeness of 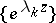 in, say,
in, say, 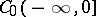 . Later, J. Korevaar, A.F. Leont'ev, P. Malliavin, J.A. Siddigi, and others studied analogous completeness problems on curves
. Later, J. Korevaar, A.F. Leont'ev, P. Malliavin, J.A. Siddigi, and others studied analogous completeness problems on curves 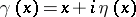 ,
, 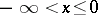 . Very recently it was shown that if
. Very recently it was shown that if 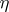 is piecewise
is piecewise 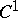 , with
, with 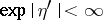 , and
, and 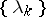 satisfies (a1) and is contained in a sufficiently small sector around the positive axis, then
satisfies (a1) and is contained in a sufficiently small sector around the positive axis, then 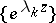 spans
spans 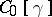 . See [a1], also for further references. Finally, attempts have been made to generalize the Müntz theorem to functions of several variables, see [a2].
. See [a1], also for further references. Finally, attempts have been made to generalize the Müntz theorem to functions of several variables, see [a2].
References
| [a1] | J. Korevaar, R. Zeinstra, "Transformées de Laplace pour les courbes à pente bornée et un résultat correspondant du type Müntz–Szász" C.R. Acad. Sci. Paris , 301 (1985) pp. 695–698 |
| [a2] | L.I. Ronkin, "Some questions of completeness and uniqueness for functions of several variables" Funct. Anal. Appl. , 7 (1973) pp. 37–45 Funkts. Anal. Prilozhen. , 7 (1973) pp. 45–55 |
Müntz theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=M%C3%BCntz_theorem&oldid=47945