Multiply-connected domain

in a path-connected space

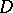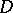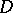A domain in which there are closed paths not homotopic to zero, or, in other words, whose fundamental group is not trivial. This means that there are closed paths in which cannot be continuously deformed to a point while remaining throughout within , or, otherwise, a multiply-connected domain is a domain which is not a simply-connected domain.

The order of connectivity of a plane doma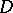in in 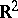or 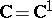(or in the compactification of these spaces, 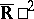or 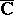) is the number of (homologically) independent one-dimensional cycles, that is, the one-dimensional Betti number 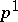of 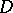. If the number 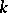of connected components of the boundary of a plane domain 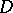, considered as a domain in the compactified space 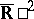or 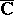, is finite, then 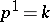; otherwise one sets 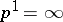. When 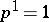, 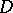is a simply-connected domain, when 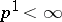it is a finitely-connected domain (one also uses such terms as doubly-connected domain, triply-connected domain 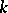-connected domain), when 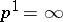, 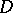is an infinitely-connected domain. All plane finitely-connected domains with equal order of connectivity, 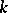, are homeomorphic to each other. By removing from such a domain 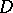all the points of 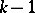cuts, that is, Jordan arcs joining pairs of connected components of the boundary, it is always possible to obtain a simply-connected domain 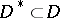. About the conformal types of plane multiply-connected domains see Riemann surfaces, conformal classes of.

The topological types of domains in 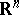, , 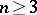or 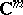, , are far more diverse and cannot be characterized by a single number. Here, sometimes, the term "multiply-connected domain" (with various provisos) is used when the fundamental group is trivial but some higher-dimensional homology group is not trivial.

Comments

For a discussion of non-planar multiply-connected domains see [a1].

There are two rather different concepts which go by the phrase "multi-connected spacemulti-connected" or "multiply-connected" . The concept and terminology as described above come from the theory of functions of a complex variable.

On the other hand, in (algebraic) topology one defines an -connected space as a space 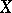such that any mapping from a sphere 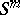, , 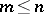into is homotopic to zero. Thus, -connectedness is the same as path connectedness.

References

[a1]	G.K. Francis, "A topological picturebook" , Springer (1987)
[a2]	W.S. Massey, "Algebraic topology: an introduction" , Springer (1967)
[a3]	G.W. Whitehead, "Elements of homotopy theory" , Springer (1978) pp. 23; 415–455