Multiple comparison

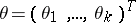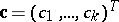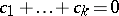The problem of testing hypotheses with respect to the values of scalar products of a vector , the coordinates of which are unknown parameters, with a number of given vectors . In statistical research the multiple comparison problem often arises in dispersion analysis where, as a rule, the vectors are chosen so that , and the scalar product 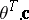itself, in this case, is called a contrast. On the assumption that are unknown mathematical expectations of one-dimensional normal laws, J.W. Tukey and H. Scheffé proposed the -method and the 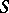-method, respectively, for the simultaneous estimation of contrasts, which are the fundamental methods in the problem of constructing confidence intervals for contrasts.

References

[1]	H. Scheffé, "The analysis of variance" , Wiley (1959)
[2]	M.G. Kendall, A. Stuart, "The advanced theory of statistics" , 3. Design and analysis, and time series , Griffin (1983)

References

[a1]	R. Miller, "Simultaneous statistical inference" , McGraw-Hill (1966)