Multi-valued representation
of a connected topological group 
An ordinary representation  of a connected topological group
of a connected topological group  (cf. Representation of a topological group) such that
(cf. Representation of a topological group) such that  is isomorphic (as a topological group) to a quotient group of
is isomorphic (as a topological group) to a quotient group of  relative to a discrete normal subgroup
relative to a discrete normal subgroup  which is not contained in the kernel of
which is not contained in the kernel of  . A multi-valued representation is called
. A multi-valued representation is called  -valued if
-valued if  contains exactly
contains exactly  elements. By identifying the elements of
elements. By identifying the elements of 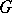 with the elements of
with the elements of 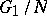 one obtains for the sets
one obtains for the sets  ,
, 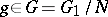 , the relations
, the relations  ,
,  ,
, 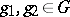 . Multi-valued representations of connected, locally path-connected topological groups
. Multi-valued representations of connected, locally path-connected topological groups 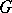 exist only for non-simply-connected groups. The most important example of a multi-valued representation is the spinor representation of the complex orthogonal group
exist only for non-simply-connected groups. The most important example of a multi-valued representation is the spinor representation of the complex orthogonal group 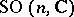 ,
, 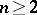 ; this representation is a two-valued representation of
; this representation is a two-valued representation of 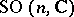 and is determined by a faithful representation of the universal covering group of
and is determined by a faithful representation of the universal covering group of 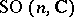 .
.
References
| [1] | A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian) |
| [2] | M.A. Naimark, "Theory of group representations" , Springer (1982) (Translated from Russian) |
Multi-valued representation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Multi-valued_representation&oldid=47924