Multi-operator group

group with multiple operators, -group

A universal algebra which is a group relative to the addition operation 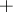(which need not be commutative) and in which there is given a system of operations of arity 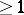. It is assumed that the zero element of the additive group 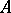is a subalgebra, that is, 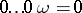for all 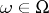. Thus, a multi-operator group combines the concepts of a group, a linear algebra and a ring. An ideal of an -group is a normal subgroup 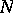of 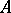such that

for all , , 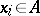, 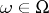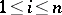. Congruences on a multi-operator group are described by coset classes relative to ideals.

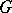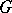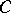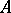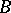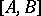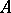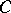Let , and be -subgroups in an -group (that is, subalgebras of the universal algebra ), where is generated by and . The mutual commutator of the subgroups and is the ideal in generated by all elements of the form

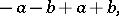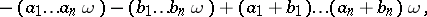where 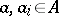, , 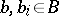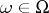. Let 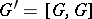. A multi-operator group 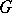is called Abelian if 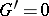. Inductively one defines ideals 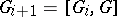, where 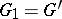, and , where 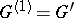. A multi-operator group 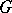is called nilpotent if 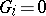, and solvable if 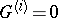for some 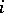. Many of the properties of the corresponding classes of groups and rings can be transferred to these classes of multi-operator groups. A multi-operator group 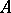is called a multi-operator (linear) -algebra over a commutative associative ring 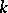with an identity if the addition in 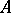is commutative, if 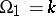, where 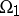is the set of unary operations from , and if all operations from are semi-linear over (see [2]–[6], and Semi-linear mapping).

References

[1]	P.J. Higgins, "Groups with multiple operators" Proc. London Math. Soc. , 6 (1956) pp. 366–416
[2]	A.G. Kurosh, "Free sums of multi-operator algebras" Sibirsk. Mat. Zh. , 1 : 1 (1960) pp. 62–70 (In Russian)
[3]	A.G. Kurosh, "Lectures on general algebra" , Chelsea (1963) (Translated from Russian)
[4]	A.G. Kurosh, "General algebra. Lectures for the academic year 1969/70" , Moscow (1974) (In Russian)
[5]	A.G. Kurosh, "Multioperator rings and algebras" Russian Math. Surveys , 24 : 1 (1969) pp. 1–13 Uspekhi Mat. Nauk. , 24 : 1 (1969) pp. 3–15
[6]	T.M. Baranovich, M.S. Burgin, "Linear -algebras" Russian Math. Surveys , 30 : 4 (1975) pp. 65–113 Uspekhi Mat. Nauk. , 30 : 4 (1975) pp. 61–106
[7]	V.A. Artamonov, "Universal algebras" Itogi Nauk. i Tekhn. Algebra. Topol. Geom. , 14 (1976) pp. 191–248 (In Russian)
[8]	, Rings , 1 , Novosibirsk (1973) pp. 41–45