Multi-dimensional distribution
multivariate distribution
A probability distribution on the  -algebra of Borel sets of an
-algebra of Borel sets of an  -dimensional Euclidean space
-dimensional Euclidean space  . One usually speaks of a multivariate distribution as the distribution of a multi-dimensional random variable, or random vector,
. One usually speaks of a multivariate distribution as the distribution of a multi-dimensional random variable, or random vector,  , meaning by this the joint distribution of the real random variables
, meaning by this the joint distribution of the real random variables  given on the same space of elementary events
given on the same space of elementary events  (
(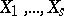 may be regarded as coordinate variables in the space
may be regarded as coordinate variables in the space  ). A multivariate distribution is uniquely determined by its distribution function — the function
). A multivariate distribution is uniquely determined by its distribution function — the function
 |
of the real variables  .
.
As in the one-dimensional case, the most widespread multivariate distributions are the discrete and the absolutely-continuous distributions. In the discrete case a multivariate distribution is concentrated on a finite or countable set of points 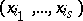 of
of  such that
such that
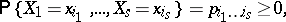 |
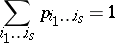 |
(see, for example, Multinomial distribution). In the absolutely-continuous case almost-everywhere (with respect to Lebesgue measure) on 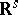 ,
,
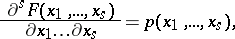 |
where  is the density of the multivariate distribution:
is the density of the multivariate distribution:
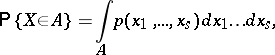 |
for any 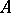 from the
from the  -algebra of Borel subsets of
-algebra of Borel subsets of  , and
, and
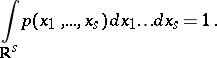 |
The distribution of any random variable 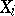 (and also, for any
(and also, for any 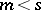 , the distribution of the variables
, the distribution of the variables 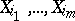 ) relative to a multivariate distribution is called a marginal distribution. The marginal distributions are completely determined by the given multivariate distribution. When
) relative to a multivariate distribution is called a marginal distribution. The marginal distributions are completely determined by the given multivariate distribution. When 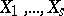 are independent, then
are independent, then
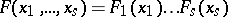 |
and
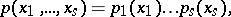 |
where 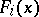 and
and 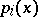 are, respectively, the marginal distribution functions and densities of the
are, respectively, the marginal distribution functions and densities of the  .
.
The mathematical expectation of any function 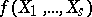 of
of 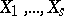 is defined by the integral of this function with respect to the multivariate distribution; in particular, in the absolutely-continuous case it is defined by the integral
is defined by the integral of this function with respect to the multivariate distribution; in particular, in the absolutely-continuous case it is defined by the integral
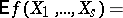 |
 |
The characteristic function of a multivariate distribution is the function of 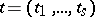 given by
given by
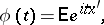 |
where 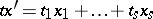 . The fundamental characteristics of a multivariate distribution are the moments (cf. Moment): the mixed moments
. The fundamental characteristics of a multivariate distribution are the moments (cf. Moment): the mixed moments  and the central mixed moments
and the central mixed moments  , where
, where  is the order of the corresponding moment. The roles of the expectation and the variance for a multivariate distribution are played by
is the order of the corresponding moment. The roles of the expectation and the variance for a multivariate distribution are played by 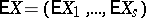 and the set of second-order central mixed moments, which form the covariance matrix. If
and the set of second-order central mixed moments, which form the covariance matrix. If 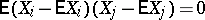 for all
for all  ,
, 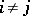 , then
, then 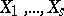 are called pairwise uncorrelated or orthogonal (the covariance matrix is diagonal). If the rank
are called pairwise uncorrelated or orthogonal (the covariance matrix is diagonal). If the rank  of the covariance matrix is less than
of the covariance matrix is less than  , then the multivariate distribution is called a degenerate distribution; in this case the distribution is concentrated on some linear manifold in
, then the multivariate distribution is called a degenerate distribution; in this case the distribution is concentrated on some linear manifold in 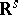 of dimension
of dimension 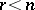 .
.
For methods of investigating dependencies between 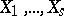 see Correlation; Regression.
see Correlation; Regression.
Comments
References
| [a1] | N.L. Johnson, S. Kotz, "Discrete distributions" , Houghton Mifflin (1969) |
| [a2] | N.L. Johnson, S. Kotz, "Continuous multivariate distributions" , Wiley (1942) |
Multi-dimensional distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Multi-dimensional_distribution&oldid=47913