Multi-algebra

A set in which a system of (in general, partial) multi-operations is given. A partial multi-operation on a set 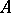is a partial mapping 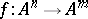between Cartesian powers of 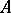, where . Here means a one-element set. A homomorphism of multi-algebras with the same system of multi-operations is a mapping 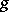such that if 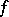is a multi-operation mapping the -th power into the 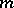-th, then

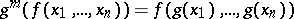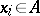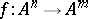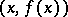for all . The concept of a multi-algebra is a generalization of that of a universal algebra. At the same time a multi-algebra is a particular case of an algebraic system, since a mapping can be identified with the -ary relation on , . Multi-algebras arise most naturally in connection with the functorial approach to universal algebra (see [1]). Namely, let 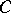be a category whose objects are the natural numbers including zero, where the object 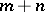is the direct product of the objects 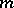and . 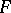Then a functor from 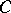into the category of sets that commutes with direct products is a multi-algebra on the set with system of multi-operations , where in 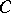. The homomorphisms in this case are precisely the natural transformations of functors.

References

[1]	F.W. Lawvere, "Functorial semantics of algebraic theories" Proc. Nat. Acad. Sci. USA , 50 : 5 (1963) pp. 869–872
[2]	V.D. Belousov, "Algebraic nets and quasi-groups" , Stiintsa , Kishinev (1971) (In Russian)