Morse function
A smooth function with certain special properties. Morse functions arise and are used in Morse theory.
Let  be a smooth complete (in some Riemannian metric) Hilbert manifold (for example, finite dimensional) whose boundary
be a smooth complete (in some Riemannian metric) Hilbert manifold (for example, finite dimensional) whose boundary  is a disconnected union (possibly empty) of manifolds
is a disconnected union (possibly empty) of manifolds  and
and  . A Morse function for the triple
. A Morse function for the triple  is a smooth (of Fréchet class
is a smooth (of Fréchet class  ) function
) function  ,
,  (or
(or  for
for  ), such that:
), such that:
1)  ,
,  ;
;
2) all critical points (cf. Critical point) of 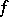 lie in
lie in  and are non-degenerate;
and are non-degenerate;
3) condition 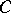 of Palais–Smale is fulfilled (see [2], [3]). I.e. on any closed set
of Palais–Smale is fulfilled (see [2], [3]). I.e. on any closed set  where
where 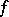 is bounded and the greatest lower bound of
is bounded and the greatest lower bound of 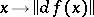 is zero, there is a critical point of
is zero, there is a critical point of 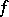 .
.
For example, if 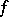 is a proper function, that is, all sets
is a proper function, that is, all sets 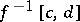 ,
, 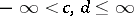 , are compact (possible only for
, are compact (possible only for  ), then
), then 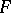 satisfies condition
satisfies condition 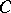 . A Morse function attains a (global) minimum on each connected component of
. A Morse function attains a (global) minimum on each connected component of 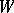 . If
. If  is a finite-dimensional manifold, then for
is a finite-dimensional manifold, then for  the set of Morse functions of class
the set of Morse functions of class  is a set of the second category (and, if
is a set of the second category (and, if 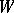 is compact, even a dense open set) in the space of all functions
is compact, even a dense open set) in the space of all functions
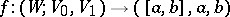 |
in the  -topology.
-topology.
References
| [1] | M. Morse, "The calculus of variations in the large" , Amer. Math. Soc. (1934) |
| [2] | R.S. Palais, "Morse theory on Hilbert manifolds" Topology , 2 (1963) pp. 299–340 |
| [3] | S. Smale, "Morse theory and a nonlinear generalization of the Dirichlet problem" Ann. of Math. , 80 (1964) pp. 382–396 |
Comments
There exist generalizations to Morse functions on stratified spaces (cf. (the editorial comments to) Morse theory and [a1]) and to equivariant Morse functions (cf. [a2] and [a3]).
References
| [a1] | M. Goreski, R. MacPherson, "Stratified Morse theory" , Springer (1988) |
| [a2] | A. Wasserman, "Morse theory for  -manifolds" Bull. Amer. Math. Soc. , 71 (1965) pp. 384–388 -manifolds" Bull. Amer. Math. Soc. , 71 (1965) pp. 384–388 |
| [a3] | A. Wasserman, "Equivariant differential topology" Topology , 8 (1969) pp. 127–150 |
Morse function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Morse_function&oldid=47902