Monodromy group

of an ordinary linear differential equation or system of equations

The group of 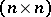-matrices associated with the -th order system

(*)

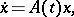defined as follows. Let the matrix 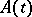be holomorphic in a domain 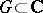, let and let be the fundamental matrix of the system (*) given in a small neighbourhood of . If 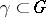is a closed curve with initial point 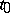, then by analytic continuation along 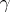, , 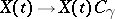where is a constant 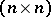-matrix. If two curves 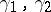are homotopic in 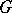, then 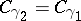; if 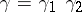, then 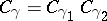. The mapping 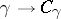is a homomorphism of the fundamental group of :

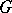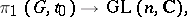where 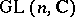is the group of 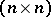-matrices with complex entries; the image of this homomorphism is called the monodromy group 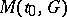of (*). In this connection,

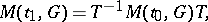where 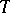is a constant matrix. The monodromy group has been computed for the equations of Euler and Papperitz (see [1], [2]).

References

[1]	V.V. Golubev, "Vorlesungen über Differentialgleichungen im Komplexen" , Deutsch. Verlag Wissenschaft. (1958) (Translated from Russian)
[2]	E.L. Ince, "Ordinary differential equations" , Dover, reprint (1956)

Comments

Cf. also Monodromy matrix and Monodromy operator. If 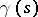is a closed differentiable curve in 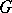with initial point 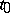, then 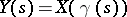satisfies a matrix equation 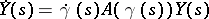and is the monodromy matrix of this system of linear differential equations with periodic coefficients.