Model, regular

An interpretation of a formal system in which all axioms are true or have the value "true" for all values of their parameters and in which the deduction rules preserve the property of taking the value "true" . This definition concerns two-valued logical calculi. If the logic is multi-valued and some of the values are distinguished, then in the definition of a regular model one has to say "taking distinguished values" instead of "taking the value true" . If the above property of a model is not satisfied, the model is said to be non-regular. Models of formal systems obtained by adjoining to restricted predicate calculus some set 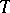of axioms are also called models of the axiom system 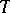or models for 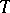. Any interpretation of such a formal system is called an algebraic system or simply a model (in logic).

Comments

In English usage, one normally distinguishes between structures for a language, which may or may not satisfy the axioms of a theory under consideration, and models, which necessarily do so; thus the term "regular model" is redundant, and is not used in this sense. See also (the editorial comments to) Algebraic system; Model (in logic).

For another use of the phrase "regular model" see [a1].

References

[a1]	J.R. Shoenfield, "Mathematical logic" , Addison-Wesley (1967)