Mixed integral equation

An integral equation that, in the one-dimensional case, has the form

(1)

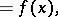where 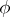is the unknown and 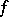is a given continuous function on 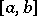, , , 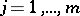are given points, and 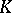, 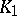are given continuous functions on the rectangle 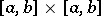. If

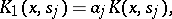where the 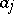are positive constants, then (1) can be written as

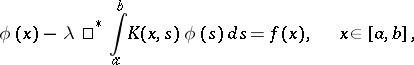(2)

where the new integration symbol, with 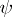an arbitrary finite integrable function, is defined by (see [1]):

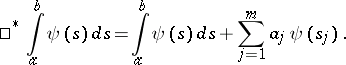The theory of Fredholm equations (cf. Fredholm equation) and, in the case of a symmetric kernel, the theory of integral equations with symmetric kernel (cf. Integral equation with symmetric kernel), is valid for equation (2).

In the case of multi-dimensional mixed integral equations, the unknown function can be part of the integrands of integrals over manifolds of different dimensions. For example, in the two-dimensional case the integral equation may have the form

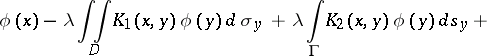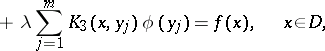where 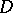is some domain in the plane, 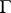is its boundary, and 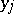are fixed points in 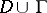. This equation may also be written as

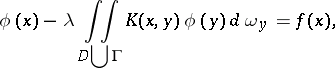if the function 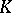and the volume element 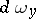are correspondingly defined. In this case, moreover, the theory of Fredholm integral equations remains valid.

References

[1]	A. Kneser, "Belastete Integralgleichungen" Rend. Circolo Mat. Palermo , 37 (1914) pp. 169–197
[2]	L. Lichtenstein, "Bemerkungen über belastete Integralgleichungen" Studia Math. , 3 (1931) pp. 212–225
[3]	N.M. Gunter, "Sur le problème des "Belastete Integralgleichungen" " Studia Math. , 4 (1933) pp. 8–14
[4]	V.I. Smirnov, "A course of higher mathematics" , 4 , Addison-Wesley (1964) (Translated from Russian)