Minkowski inequality
The proper Minkowski inequality: For real numbers 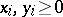 ,
, 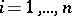 , and for
, and for  ,
,
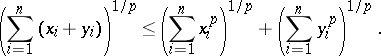 | (1) |
This was derived by H. Minkowski . For 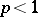 ,
, 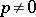 , the inequality is reversed (for
, the inequality is reversed (for 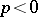 one must have
one must have  ). In each case equality holds if and only if the rows
). In each case equality holds if and only if the rows 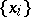 and
and 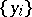 are proportional. For
are proportional. For 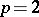 Minkowski's inequality is called the triangle inequality. Minkowski's inequality can be generalized in various ways (also called Minkowski inequalities). Below some of them are listed.
Minkowski's inequality is called the triangle inequality. Minkowski's inequality can be generalized in various ways (also called Minkowski inequalities). Below some of them are listed.
Minkowski's inequality for sums. Let  for
for 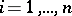 and
and 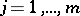 and let
and let 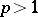 . Then
. Then
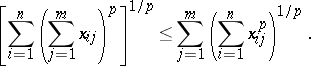 | (2) |
The inequality is reversed for  ,
, 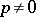 , and for
, and for 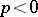 it is assumed that
it is assumed that 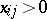 . In each case equality holds if and only if the rows
. In each case equality holds if and only if the rows 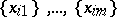 are proportional. There are also generalizations of
are proportional. There are also generalizations of
for multiple and infinite sums. However, when limit processes are used special attention is required in formulating the case of possible equality (see ).
Inequalities
and (2) are homogeneous with respect to  and therefore have analogues for various means, for example, if
and therefore have analogues for various means, for example, if 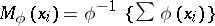 , where
, where 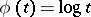 , then
, then
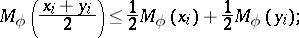 |
for more details see .
Minkowski's inequality for integrals is similar to
and also holds because of the homogeneity with respect to 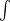 . Let
. Let 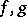 be integrable functions in a domain
be integrable functions in a domain 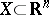 with respect to the volume element
with respect to the volume element 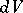 . Then for
. Then for 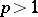 ,
,
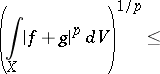 | (3) |
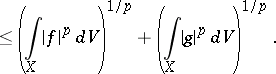 |
A generalization of (3) to more general functions can be obtained naturally. A further generalization is: If 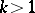 , then
, then
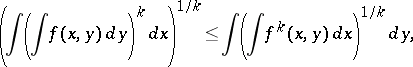 |
where equality holds only if 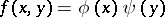 .
.
Other inequalities of Minkowski type:
a) for products: If 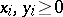 , then
, then
 |
b) Mahler's inequality: Let 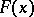 be a generalized norm on
be a generalized norm on 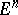 and
and 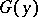 its polar function; then
its polar function; then
 |
where 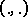 is the inner product;
is the inner product;
c) for determinants: If 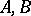 are non-negative Hermitian matrices over
are non-negative Hermitian matrices over 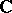 , then
, then
 |
Finally, connected with the name of Minkowski are other inequalities; in particular, in convex analysis and number theory. For example, the Brunn–Minkowski theorem.
References
| [1] | H. Minkowski, "Geometrie der Zahlen" , Chelsea, reprint (1953) |
| [2] | G.H. Hardy, J.E. Littlewood, G. Pólya, "Inequalities" , Cambridge Univ. Press (1934) |
| [3] | E.F. Beckenbach, R. Bellman, "Inequalities" , Springer (1961) |
| [4] | M. Marcus, H. Minc, "Survey of matrix theory and matrix inequalities" , Allyn & Bacon (1964) |
Comments
A generalized norm on 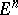 is a function
is a function 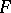 for which: 1)
for which: 1) 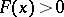 for
for 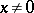 ; 2)
; 2) 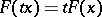 for
for 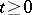 ; and 3)
; and 3)  . The polar form (or polar function)
. The polar form (or polar function) 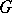 of the generalized norm
of the generalized norm 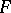 is defined by:
is defined by:
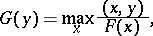 |
where 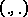 is the inner product.
is the inner product.
References
| [a1] | P.S. Bullen, D.S. Mitrinović, P.M. Vasić, "Means and their inequalities" , Reidel (1988) |
Minkowski inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Minkowski_inequality&oldid=47853