Minkowski hypothesis

on the product of inhomogeneous linear forms

A statement according to which for real linear forms

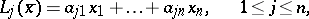in variables , with a non-zero determinant 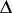, and any real , there are integers such that the inequality

(*)

holds. This hypothesis was proved by H. Minkowski (1918) in case 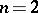. A proof of the hypothesis is known (1982) for 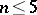, and (*) has been proved for 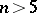under certain additional restrictions (see [2]).

References

[1]	J.W.S. Cassels, "An introduction to the geometry of numbers" , Springer (1972)
[2]	B.F. Skubenko, "A proof of Minkowski's conjecture on the product of linear inhomogeneous forms in variables for " , Investigations in number theory , Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. Steklov , 33 (1973) pp. 6–36 (In Russian)

Comments

See also Geometry of numbers.

References

[a1]	P.M. Gruber, C.G. Lekkerkerker, "Geometry of numbers" , North-Holland (1987) pp. Sect. (iv) (Updated reprint)
[a2]	P. Erdös, P.M. Gruber, J. Hammer, "Lattice points" , Longman (1989)