Minimization of an area
The problem of finding the minimum of the area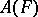 
of a Riemann surface to which a given domain 
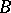of the 
-plane is mapped by a one-to-one regular function 
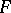of a given class 
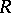, that is, the problem of finding
 | (*) |
(
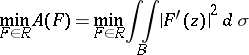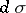is the surface element). The integral in (*), taken over 
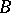, is understood as the limit of integrals over domains 
, 
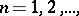which exhaust the domain 
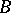, that is, are such that 
, 
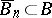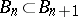and such that any closed set 
lies in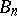 
from some 
onwards.
When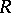 
is the class of functions 
, 
, 
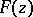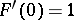, regular in a given simply-connected domain 
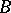containing 
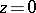and having more than one boundary point, the minimum 
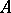of the areas 
of the images of 
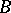in the class 
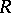is given by the unique function univalently mapping 
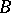onto the full disc 
, where 
is the conformal radius of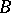 
at 
(cf. Conformal radius of a domain); moreover,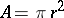 
.
The problem of finding the minimal area of the image of a multiply-connected domain has also been considered (see [1]).
References
| [1] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
Minimization of an area. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Minimization_of_an_area&oldid=47848