Minimal sufficient statistic
A statistic  which is a sufficient statistic for a family of distributions
which is a sufficient statistic for a family of distributions  and is such that for any other sufficient statistic
and is such that for any other sufficient statistic  ,
,  , where
, where  is some measurable function. A sufficient statistic is minimal if and only if the sufficient
is some measurable function. A sufficient statistic is minimal if and only if the sufficient  -algebra it generates is minimal, that is, is contained in any other sufficient
-algebra it generates is minimal, that is, is contained in any other sufficient  -algebra.
-algebra.
The notion of a  -minimal sufficient statistic (or
-minimal sufficient statistic (or  -algebra) is also used. A sufficient
-algebra) is also used. A sufficient 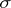 -algebra
-algebra  (and the corresponding statistic) is called
(and the corresponding statistic) is called  -minimal if
-minimal if  is contained in the completion
is contained in the completion  , relative to the family of distributions
, relative to the family of distributions  , of any sufficient
, of any sufficient 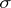 -algebra
-algebra  . If the family
. If the family  is dominated by a
is dominated by a  -finite measure
-finite measure  , then the
, then the  -algebra
-algebra  generated by the family of densities
generated by the family of densities
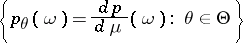 |
is sufficient and  -minimal.
-minimal.
A general example of a minimal sufficient statistic is given by the canonical statistic  of an exponential family
of an exponential family
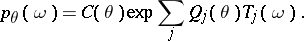 |
References
| [1] | J.-R. Barra, "Mathematical bases of statistics" , Acad. Press (1981) (Translated from French) |
| [2] | L. Schmetterer, "Introduction to mathematical statistics" , Springer (1974) (Translated from German) |
Comments
References
| [a1] | E.L. Lehmann, "Theory of point estimation" , Wiley (1983) |
| [a2] | E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1986) |
Minimal sufficient statistic. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Minimal_sufficient_statistic&oldid=47843