Minimal property
From Encyclopedia of Mathematics
of the partial sums of an orthogonal expansion
For any function 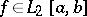 , any orthonormal system
, any orthonormal system  on
on 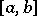 and for any
and for any  , the equality
, the equality
 |
 |
holds, where
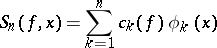 |
is the  -th partial sum of the expansion of
-th partial sum of the expansion of 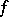 with respect to the system
with respect to the system  , that is,
, that is,
 |
The minimum is attained precisely at the sum  and
and
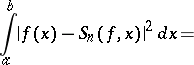 |
 |
Bessel's inequality, Parseval's equality for complete systems and also certain other basic properties of orthogonal expansions essentially are corollaries of this equality (cf. Bessel inequality; Parseval equality; Complete system of functions; Orthogonal series; Orthogonal system).
References
| [1] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) |
| [2] | S. Kaczmarz, H. Steinhaus, "Theorie der Orthogonalreihen" , Chelsea, reprint (1951) |
Comments
References
| [a1] | K. Yosida, "Functional analysis" , Springer (1978) pp. Sect. III.4 |
How to Cite This Entry:
Minimal property. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Minimal_property&oldid=47842
Minimal property. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Minimal_property&oldid=47842
This article was adapted from an original article by A.A. Talalyan (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article