Mercer theorem
From Encyclopedia of Mathematics
The bilinear series
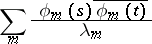 |
of a Hermitian positive-definite continuous kernel 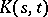 on
on 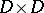 (cf. Integral equation with symmetric kernel; Kernel of an integral operator), where
(cf. Integral equation with symmetric kernel; Kernel of an integral operator), where 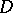 is the closure of a bounded domain in
is the closure of a bounded domain in 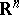 , converges absolutely and uniformly in
, converges absolutely and uniformly in 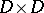 to
to 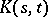 . Here the
. Here the 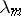 are the characteristic numbers of the kernel
are the characteristic numbers of the kernel 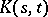 and the
and the 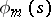 are the corresponding orthonormalized eigen functions. If a kernel
are the corresponding orthonormalized eigen functions. If a kernel 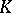 satisfies the conditions of Mercer's theorem, then the integral operator
satisfies the conditions of Mercer's theorem, then the integral operator 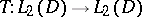 ,
,
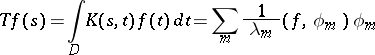 |
is nuclear (cf. Nuclear operator) and its trace 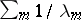 can be calculated by the formula
can be calculated by the formula
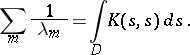 |
Mercer's theorem can be generalized to the case of a bounded discontinuous kernel.
The theorem was proved by J. Mercer [1].
References
| [1] | J. Mercer, Philos. Trans. Roy. Soc. London Ser. A , 209 (1909) pp. 415–446 |
| [2] | J. Mercer, "Functions of positive and negative type, and their connection with the theory of integral equations" Proc. Roy. Soc. London Ser. A , 83 (1908) pp. 69–70 |
| [3] | I.G. Petrovskii, "Lectures on the theory of integral equations" , Graylock (1957) (Translated from Russian) |
| [4] | F.G. Tricomi, "Integral equations" , Interscience (1957) |
| [5] | M.A. Krasnosel'skii, et al., "Integral operators in spaces of summable functions" , Noordhoff (1976) (Translated from Russian) |
Comments
References
| [a1] | I.C. Gohberg, S. Goldberg, "Basic operator theory" , Birkhäuser (1977) |
| [a2] | A.C. Zaanen, "Linear analysis" , North-Holland (1956) |
How to Cite This Entry:
Mercer theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mercer_theorem&oldid=47822
Mercer theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mercer_theorem&oldid=47822
This article was adapted from an original article by V.B. Korotkov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article