Maximum-entropy spectral estimator
auto-regressive spectral estimator
An estimator 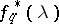 for the spectral density
for the spectral density 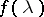 of a discrete-time stationary stochastic process such that 1) the first
of a discrete-time stationary stochastic process such that 1) the first 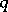 values of the auto-correlations are equal to the sample auto-correlations calculated from the observational data, and 2) the entropy of the Gaussian stochastic process with spectral density
values of the auto-correlations are equal to the sample auto-correlations calculated from the observational data, and 2) the entropy of the Gaussian stochastic process with spectral density 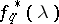 is maximized subject to condition 1). If
is maximized subject to condition 1). If 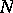 sample values
sample values 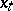 ,
, 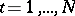 , are known from observing a realization of a real stationary process
, are known from observing a realization of a real stationary process 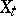 having spectral density
having spectral density 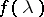 , then the maximum-entropy spectral estimator
, then the maximum-entropy spectral estimator 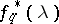 is defined by the relations
is defined by the relations
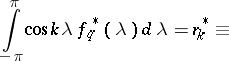 | (1) |
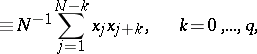 |
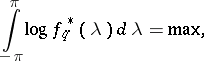 | (2) |
where the sign  denotes "equal by definition" . The maximum-entropy spectral estimator has the form
denotes "equal by definition" . The maximum-entropy spectral estimator has the form
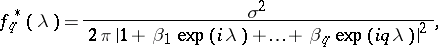 | (3) |
where the coefficients 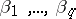 and
and 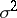 are given by the
are given by the 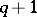 equations (1) (see, e.g., [1], [9], [10]). Formula (3) shows that the maximum-entropy spectral estimator coincides with the so-called auto-regressive spectral estimator (introduced in [2], [3]). The positive integer
equations (1) (see, e.g., [1], [9], [10]). Formula (3) shows that the maximum-entropy spectral estimator coincides with the so-called auto-regressive spectral estimator (introduced in [2], [3]). The positive integer 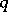 here plays a role related to that played by the reciprocal width of a spectral window in the case of non-parametric estimation of the spectral density by periodogram smoothing (see Spectral window; Statistical problems in the theory of stochastic processes). There are several methods for estimating the optimal value of
here plays a role related to that played by the reciprocal width of a spectral window in the case of non-parametric estimation of the spectral density by periodogram smoothing (see Spectral window; Statistical problems in the theory of stochastic processes). There are several methods for estimating the optimal value of 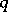 from given observations (see, for example, [1], [4], [5], [8]). The values of the coefficients
from given observations (see, for example, [1], [4], [5], [8]). The values of the coefficients 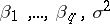 can be found using a solution of the Yule–Walker equations
can be found using a solution of the Yule–Walker equations
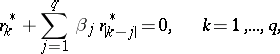 | (4) |
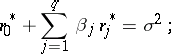 | (5) |
there are also other, numerically more convenient, methods for calculating these coefficients (see, e.g., [1], [4]–[6], [10]).
In the case of small sample size or spectral densities of complex form, maximum-entropy spectral estimators and parametric spectral estimators (cf. Spectral estimator, parametric), which generalize them, possess definite advantages over non-parametric estimators of 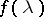 : they usually have a more regular form and possess better resolving power, that is, they permit one to better distinguish close peaks of the graph of the spectral density (see [1], [4]–[7]). Therefore maximum-entropy spectral estimators are widely used in the applied spectral analysis of a stationary stochastic process.
: they usually have a more regular form and possess better resolving power, that is, they permit one to better distinguish close peaks of the graph of the spectral density (see [1], [4]–[7]). Therefore maximum-entropy spectral estimators are widely used in the applied spectral analysis of a stationary stochastic process.
References
| [1] | D.G. Childers (ed.) , Modern spectrum analysis , IEEE (1978) |
| [2] | E. Parzen, "An approach to empirical time series analysis" Radio Sci. , 68 (1964) pp. 937–951 |
| [3] | H. Akaike, "Power spectrum estimation through autoregressive model fitting" Ann. Inst. Stat. Math. , 21 : 3 (1969) pp. 407–419 |
| [4] | S.S. Haykin (ed.) , Nonlinear methods of spectral analysis , Springer (1979) |
| [5] | S.M. Kay, S.L. Marpl, "Spectrum analysis—a modern perspective" Proc. IEEE , 69 : 11 (1981) pp. 1380–1419 |
| [6] | "Spectral estimation" Proc. IEEE , 70 : 9 (1982) ((Special Issue)) |
| [7] | V.F. Pisarenko, "Sampling properties of maximum entropy spectral estimation" , Numerical Seismology , Moscow (1977) pp. 118–149 (In Russian) |
| [8] | J.G. de Gooyer, B. Abraham, A. Gould, L. Robinson, "Methods for determining the order of an autoregressive-moving average process: A survey" Internat. Stat. Rev. , 55 (1985) pp. 301–329 |
| [9] | M.B. Priestley, "Spectral analysis and time series" , 1–2 , Acad. Press (1981) |
| [10] | A. Papoulis, "Probability, random variables and stochastic processes" , McGraw-Hill (1984) |
Maximum-entropy spectral estimator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximum-entropy_spectral_estimator&oldid=47804