Mapping, principal net of a
From Encyclopedia of Mathematics
in a domain of a mapping
An orthogonal net in a domain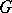 
of an 
-dimensional manifold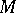 
(which can be, in particular, a Euclidean space) that is mapped onto a net, also orthogonal, by a diffeomorphism 
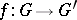of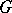 
onto a domain 
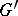in the same or another Riemannian manifold 
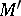. The directions tangential to the lines of the principal net of the mapping at the point 
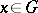are the principal directions of the ellipsoid of deformation of the induced mapping 
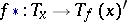of the tangent space 
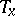onto the tangent space 
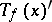. When 
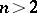, generally speaking, the principal net of a mapping is not holonomic. If the mapping 
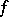is conformal, then any orthogonal net in the domain 
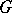serves as a principal net.
References
| [1] | V.V. Ryzhkov, "Differential geometric point correspondences between spaces" Itogi Nauk. Ser. Mat. Geom. 1963 , 3 (1965) pp. 65–107 (In Russian) |
How to Cite This Entry:
Mapping, principal net of a. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mapping,_principal_net_of_a&oldid=47756
Mapping, principal net of a. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mapping,_principal_net_of_a&oldid=47756
This article was adapted from an original article by V.T. Bazylev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article