Lyapunov stochastic function

A non-negative function 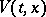for which the pair 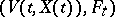is a supermartingale for some random process 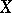up to the instant 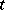(cf. also Martingale). If 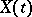is a Markov process, then the Lyapunov stochastic function is a function for which the Lyapunov stochastic operator

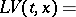is non-positive. The operator 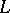is the infinitesimal operator of the process 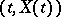, and so the verification of the condition 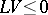is easily carried out in specific cases. The operator goes into the usual Lyapunov operator when the process is determinate and is described by a system of differential equations. By means of the Lyapunov stochastic function it is possible to verify a number of qualitative properties of the trajectories of 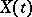; their role in the theory of random processes is similar to the role of the classical Lyapunov function in the theory of systems of differential equations.

Functions 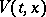for which 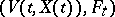is not a supermartingale, but from which one can readily form a supermartingale, are sometimes also called Lyapunov stochastic functions. Below typical results are presented on the qualitative behaviour of trajectories of Markov processes in terms of a Lyapunov stochastic function.

1) If 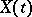is a right-continuous strong Markov process in 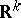, defined up to the instant of first leaving an arbitrary compact set, and if there is a Lyapunov stochastic function 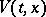, , 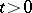, 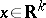and a constant such that

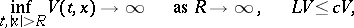then

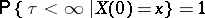for any 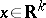; that is, the process 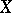is defined for all 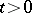(is indefinitely extendable).

2) For the stationary Markov process in 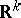corresponding to a transition function 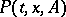to exist it is sufficient that there should be a function 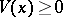for which

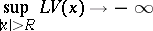as .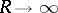

By means of the Lyapunov stochastic function one can carry over to Markov processes the main theorems of the direct Lyapunov method; these functions have also found application in the investigation of processes in discrete time.

References

[1]	H.J. Kushner, "Stochastic stability and control" , Acad. Press (1967)
[2]	R.Z. [R.Z. Khas'minskii] Has'minskii, "Stochastic stability of differential equations" , Sijthoff & Noordhoff (1980) (Translated from Russian)
[3]	V.V. Kalashnikov, "Qualitative analysis of the behaviour of complex systems by the method of test functions" , Moscow (1978) (In Russian)

Comments

The phrase stochastic Lyapunov function is more common than "Lyapunov stochastic function" .

Recently, stochastic Lyapunov functions have been used to prove convergence of recursive algorithms driven by stochastic processes. Convergence problems of this type arise in system identification and adaptive control.

References

[a1]	G.C. Goodwin, P.J. Ramagadge, P.E. Caines, "Discrete time stochastic adaptive control" SIAM J. Control Optim. , 19 (1981) pp. 829–853
[a2]	M. Metivier, P. Priouret, "Applications of a Kushner and Clark lemma to general classes of stochastic algorithms" IEEE Trans. Inform. Theory , 30 (1984) pp. 140–151
[a3]	V. Solo, "The convergence of AML" IEEE Trans. Autom. Control , 24 (1979) pp. 958–962
[a4]	J.H. van Schuppen, "Convergence results for continuous-time stochastic filtering algorithms" J. Math. Anal. Appl. , 96 (1983) pp. 209–225