Lyapunov function

A function defined as follows. Let be a fixed point of the system of differential equations

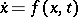(that is, ), where the mapping is continuous and continuously differentiable with respect to (here is a neighbourhood of in ). In coordinates this system is written in the form

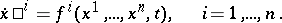A differentiable function 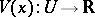is called a Lyapunov function if it has the following properties:

1) 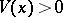for ;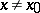

2) ;

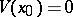3)

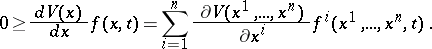The function 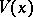was introduced by A.M. Lyapunov (see [1]).

Lyapunov's lemma holds: If a Lyapunov function exists, then the fixed point is Lyapunov stable (cf. Lyapunov stability). This lemma is the basis for one of the methods for investigating stability (the so-called second method of Lyapunov).

References

[1]	A.M. Lyapunov, "Stability of motion" , Acad. Press (1966) (Translated from Russian)
[2]	E.A. Barbashin, "Lyapunov functions" , Moscow (1970) (In Russian)

Comments

For additional references see Lyapunov stability.