Lyapunov-Schmidt equation
A non-linear integral equation of the form
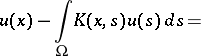 | (1) |
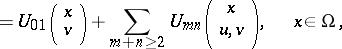 |
where
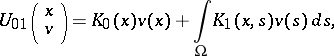 |
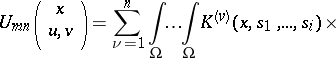 |
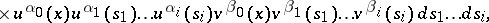 |
 ,
, 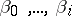 are non-negative integers,
are non-negative integers,
 |
 is a closed bounded set in a finite-dimensional Euclidean space,
is a closed bounded set in a finite-dimensional Euclidean space,  and the function
and the function 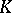 are given continuous functions of their arguments,
are given continuous functions of their arguments, 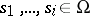 , and
, and  is the unknown function. The sum on the right-hand side of (1) may be finite or it may represent an infinite series. In the latter case the series is called an integro-power series of two functional arguments. It is assumed that the series converges absolutely and uniformly.
is the unknown function. The sum on the right-hand side of (1) may be finite or it may represent an infinite series. In the latter case the series is called an integro-power series of two functional arguments. It is assumed that the series converges absolutely and uniformly.
If 1 is not a characteristic number of the kernel 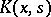 , then equation (1) has a unique small solution in the class of continuous functions for sufficiently small
, then equation (1) has a unique small solution in the class of continuous functions for sufficiently small 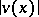 . This solution can be represented as an integro-power series. The case when 1 is a characteristic number of the kernel
. This solution can be represented as an integro-power series. The case when 1 is a characteristic number of the kernel 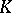 is more complicated. In this case one constructs a system of equations — the branching equations (bifurcation equations):
is more complicated. In this case one constructs a system of equations — the branching equations (bifurcation equations):
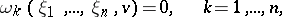 | (2) |
where 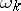 are known power series and
are known power series and  is the multiplicity of the characteristic number 1. In the general case the system (2) has a non-unique solution. Whatever the fixed sufficiently small function
is the multiplicity of the characteristic number 1. In the general case the system (2) has a non-unique solution. Whatever the fixed sufficiently small function  , to every small continuous solution of (2) (a continuous solution of (2) is said to be small if
, to every small continuous solution of (2) (a continuous solution of (2) is said to be small if 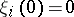 ) there corresponds a small solution of (1) that can be represented as an integro-power series.
) there corresponds a small solution of (1) that can be represented as an integro-power series.
An equation of the type (1) was first considered by A.M. Lyapunov in 1906, and later — in a more general form — by E. Schmidt in 1908.
References
| [1] | M.M. Vainberg, V.A. Trenogin, "Theory of branching of solutions of non-linear equations" , Noordhoff (1974) (Translated from Russian) |
| [2] | N.S. Smirnov, "Introduction to the theory of integral equations" , Moscow-Leningrad (1936) (In Russian) |
Comments
References
| [a1] | S.-N. Chow, J.K. Hale, "Methods of bifurcation theory" , Springer (1982) |
Lyapunov-Schmidt equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lyapunov-Schmidt_equation&oldid=47726