Luzin problem

A problem in the theory of trigonometric series. It consists in proving Luzin's conjecture, stating that the Fourier series

(*)

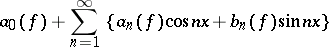of a Lebesgue-measurable function 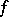, defined on the interval 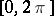, with finite integral

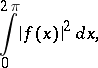converges almost everywhere on 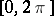. The conjecture was made by N.N. Luzin in 1915 in his dissertation (see [1]). Luzin's problem was solved in 1966 in the affirmative sense by L. Carleson (see Carleson theorem). Until Carleson's paper [2] it was not even known whether the Fourier series of a continuous function on the interval 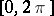converges at least at one point.

References

[1]	N.N. Luzin, "The integral and trigonometric series" , Moscow-Leningrad (1953) pp. 219 (In Russian) (Thesis; also: Collected Works, Vol. 1, Moscow, 1953, pp. 48–212)
[2]	L. Carleson, "Convergence and growth of partial sums of Fourier series" Acta Math. , 116 (1966) pp. 135–157

B.S. Kashin

One of a number of fundamental problems in set theory posed by N.N. Luzin [1], for the solution of which he proposed the method of resolvents. Namely, a problem 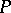of set theory is posed in a resolvent if one can indicate a set of points 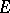such that 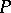is solved affirmatively every time one can indicate a point of 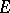, and is solved negatively if one can prove that 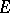is empty. The set 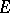itself is called the resolvent of the problem .

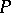Problem 1. Are all co-analytic sets (cf. 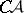-set) countable or do they have the cardinality of the continuum? The resolvent 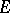of this problem is a Luzin set of class at most 3; that is, if one can find a point of 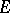, then there is an uncountable co-analytic set without perfect part, while if 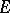is empty, then there are no such co-analytic sets.

Problem 2. Do there exists Lebesgue-unmeasurable Luzin sets?

Problem 3. Does there exist a Luzin set without the Baire property?

Luzin conjectured that the Problems 1, 2, 3 are undecidable. This conjecture has been confirmed (see [3], [4]). Connections between these problems have been established. For example, from the existence of an unmeasurable set of type 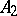follows the existence of an uncountable set of type 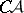not containing a perfect subset. I. Novak [5] obtained an affirmative solution of Luzin's problem about parts of the series of natural numbers, starting from the continuum hypothesis or the negation of the Luzin hypothesis.

References

[1]	N.N. [N.N. Luzin] Lusin, "Sur le problème de M. Emile Borel et la méthode des résolvants" C.R. Acad. Sci. Paris , 181 (1925) pp. 279–281
[2]	N.N. Luzin, "Collected works" , 2 , Moscow (1958) (In Russian)
[3]	P.S. Novikov, "On the non-contradictibility of certain propositions in descriptive set theory" Trudy Mat. Inst. Steklov. , 38 (1951) pp. 279–316 (In Russian)
[4]	R. Solovay, "A model of set theory in which every set of reals is Lebesgue measurable" Ann. of Math. (2) , 92 : 1 (1970) pp. 1–56
[5]	J. Novak, "On some problems of Lusin concerning the subsets of natural numbers" Czechoslovak. Math. J. , 3 (1953) pp. 385–395

B.A. Efimov

Comments

See Luzin set for usual terminology. For other problems of Luzin see Luzin theorem.

References

[a1]	T.J. Jech, "Set theory" , Acad. Press (1978) pp. Chapt. 7 (Translated from German)
[a2]	Y.N. Moschovakis, "Descriptive set theory" , North-Holland (1980)