Luxemburg norm
From Encyclopedia of Mathematics
A function
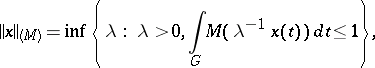 |
where 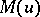 is an even convex function that increases for positive
is an even convex function that increases for positive  ,
,
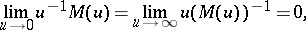 |
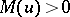 for
for 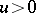 , and
, and 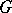 is a bounded set in
is a bounded set in 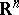 . The properties of this norm were studied by W.A.J. Luxemburg [1]. The Luxemburg norm is equivalent to the Orlicz norm (see Orlicz space), and
. The properties of this norm were studied by W.A.J. Luxemburg [1]. The Luxemburg norm is equivalent to the Orlicz norm (see Orlicz space), and
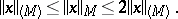 |
If the functions 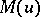 and
and 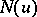 are complementary (or dual) to each other (see Orlicz class), then
are complementary (or dual) to each other (see Orlicz class), then
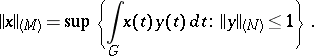 |
If 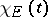 is the characteristic function of a measurable subset
is the characteristic function of a measurable subset 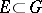 , then
, then
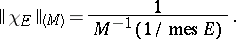 |
References
| [1] | W.A.J. Luxemburg, "Banach function spaces" , T.U. Delft (1955) (Thesis) |
| [2] | M.A. Krasnosel'skii, Ya.B. Rutitskii, "Convex functions and Orlicz spaces" , Noordhoff (1961) (Translated from Russian) |
How to Cite This Entry:
Luxemburg norm. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Luxemburg_norm&oldid=47719
Luxemburg norm. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Luxemburg_norm&oldid=47719
This article was adapted from an original article by E.M. Semenov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article