Lower bound of a family of topologies

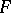(given on a single set )

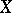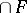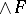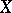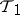The set-theoretical intersection of this family, that is, . It is usually denoted by and is always a topology on . If and 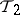are two topologies on 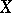and if 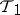is contained (as a set) in 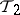, then one writes .

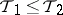The topology 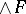has the following property: If 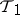is a topology on and if 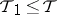for all 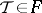, then 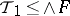. The free sum of the spaces that are obtained when all the individual topologies in 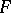are put on 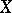can be mapped canonically onto the space 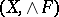. An important property of this mapping is that it is a quotient mapping. On this basis one proves general theorems on the preservation of a number of properties under the operation of intersecting topologies.

References

[1]	A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) (Translated from Russian)

Comments

The article above actually defines the infimum of the family of topologies, which is a particular (the largest) lower bound for the family; a lower bound being any topology 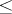this infimum.