Longman method

A method for the approximate calculation of a definite integral

where has exactly roots 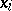inside the interval ,

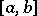and satisfies the conditions stated below. Let

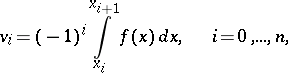then 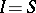, where

It is assumed that preserves its sign on the interval , has different signs on adjacent intervals, and 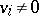, . Such a function is said to be oscillatory. The calculation of 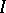by means of a quadrature formula for large is difficult, since a good approximation of an oscillatory function on the whole interval 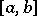is impossible in practice. The use of the equality 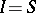leads to the need to calculate all integrals , which is also inadvisable in the case of large .

The approximate calculation of 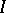in Longman's method is based on the equality ()

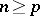(1)

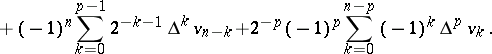In (1) the finite differences of 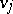as functions of the discrete argument 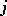occur:

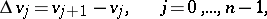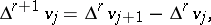If is such that on the right-hand side of (1) one can neglect terms containing finite differences of order , then the approximate equality

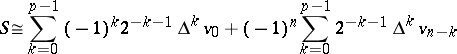(2)

can be used to calculate . To calculate the right-hand side of (2) it is sufficient to know the first 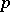values 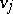, that is, the values , and the last 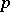values . Longman's method consists in the use of (2) for an approximate calculation of the sum .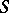

If in the integral 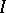the upper limit of integration 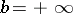and

then instead of (1) one must use the equality

(the Euler transform) and replace the series on the right-hand side by a partial sum.

The method was proposed by I.M. Longman [1].

References

[1]	I.M. Longman, "A method for the numerical evaluation of finite integrals of oscillatory functions" Math. Comput. , 14 : 69 (1960) pp. 53–59
[2]	P.J. Davis, P. Rabinowitz, "Methods of numerical integration" , Acad. Press (1984)