Logistic distribution

A probability distribution with distribution function , where is scale parameter, is a shift and

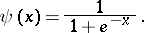The function satisfies the differential equation

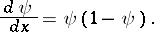The logistic distribution is close to the normal distribution:

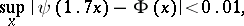where is the normal distribution function with mean and variance 1. To test the hypothesis of coincidence of the distribution functions of two samples of a logistic distribution with possibly different shifts the Wilcoxon test (the Mann–Whitney test) is asymptotically optimal. The logistic distribution is sometimes more convenient than the normal distribution in data processing and the interpretation of inferences. In applications the multi-dimensional logistic distribution is also used.

References

[1]	M.G. Kendall, A. Stuart, "The advanced theory of statistics" , 2. Inference and relationship , Griffin (1979)
[2]	D.R. Cox, D.V. Hinkley, "Theoretical statistics" , Chapman & Hall (1974)

References

[a1]	N.L. Johnson, S. Kotz, "Distributions in statistics" , 1. Continuous univariate distributions , Wiley (1970)